题目内容

直角三角形的两直角边长分别为12、16，则它的斜边上的高是（　　）
A．6B．
30
15
C．
48
5
D．
60
13
由勾股定理可得：斜边长2=162+122，
则斜边长=20，
直角三角形面积S=
1
2
×16×12=
1
2
×20×斜边的高，
可得：斜边的高=
48
5
，
故选C．
练习册系列答案
相关题目
如图是连江新华都超市一楼与二楼之间的手扶电梯示意图．其中AB、CD分别表示一楼、二楼地面的水平线，小马虎从点A到点C共走了12m，电梯上升的高度h为6m，经小马虎测量AB=2m，则BE=______m．
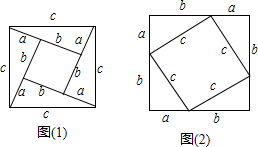如图，利用图（1）或图（2）两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理，这个定理结论的数学表达式是______．
已知：Rt△ABC中，∠C=90°．
（1）如图（1）以Rt△ABC的三边为直径的三个半圆面积分别表示为S1、S2、S3，则：S1、S2、S3之间有什么关系？证明你的结论．
（2）如图（2），将图（1）的面积为S3的半圆沿斜边AB所在的直线翻折，翻折后的半圆恰好经过直角顶点C，若AB=5，AC=4，请你利用（1）中的结论求出图（2）中阴影部分的面积．
如图，△ABC与△ADE都是以A为直角顶点的等腰直角三角形，DE交AC于点F，且AB=5，AD=3
2
．当△CEF是直角三角形时，BD=______．
在△ABC中，已知∠A=60°，AB=2，AC=3，试求△ABC的面积．
如图，为测得到池塘两岸点A和点B间的距离，一个观测者在C点设桩，使∠ABC=90°，并测得AC长5米、BC长4米，则A、B两点间距离是______米．
△ABC中，∠ACB=90°，CD⊥AB于点D，AD、DB的长是方程x2-20x+m=0的根，若△ABC的面积为40，则m=______．
平平湖水清可鉴，面上半尺生红莲；出泥不染亭亭立，忽被强风吹一边，渔人观看忙向前，花离原位二尺远；能算诸君请解题，湖水如何知深浅？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网