题目内容
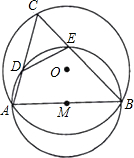
已知⊙O的半径为r,AB、CD为⊙O的两条直径,且弧AC=60°,P为弧BC上的任意一点,PA、PD分别交CD、AB于E、F,则AE•AP+DF•DP等于
- A.3r2
- B.
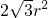
- C.4r2
- D.
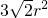
A
分析:由AB,CD是直径,弧AC为60°,可以证明△ACE和△DOF全等,得到对应边相等.由两组三角形相似,对应线段成比例,得到线段乘积的形式,然后结合图形进行计算.
解答:如图:
∵ =60°,CD为直径,
=60°,CD为直径,
∴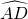 =120°,∴∠C=60°=∠P.
=120°,∴∠C=60°=∠P.
在△ACE和△D0F中,
AC=OC=DO
∠C=∠DOF=60°
∠CAE=∠ODF
∴△ACE≌△DOF
∴CE=OF.
又∵△AOE∽△APF,△DOF∽△DPE
∴AE•AP=AO•AF,DF•DP=DO•DE.
∴AE•AP+DF•DP
=AO•AF+DO•DE
=r(r+OF)+r(r+OE)
=r(2r+OE+OF)
=r(2r+OE+CE)
=r(2r+r)
=3r2.
故选A.
点评:本题考查的是垂径定理,根据直径和弧的度数,得到两三角形全等,对应边相等.由三角形相似,对应线段成比例,得到线段乘积的形式,结合图形计算求值.
分析:由AB,CD是直径,弧AC为60°,可以证明△ACE和△DOF全等,得到对应边相等.由两组三角形相似,对应线段成比例,得到线段乘积的形式,然后结合图形进行计算.
解答:如图:

∵
 =60°,CD为直径,
=60°,CD为直径,∴
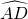 =120°,∴∠C=60°=∠P.
=120°,∴∠C=60°=∠P.在△ACE和△D0F中,
AC=OC=DO
∠C=∠DOF=60°
∠CAE=∠ODF
∴△ACE≌△DOF
∴CE=OF.
又∵△AOE∽△APF,△DOF∽△DPE
∴AE•AP=AO•AF,DF•DP=DO•DE.
∴AE•AP+DF•DP
=AO•AF+DO•DE
=r(r+OF)+r(r+OE)
=r(2r+OE+OF)
=r(2r+OE+CE)
=r(2r+r)
=3r2.
故选A.
点评:本题考查的是垂径定理,根据直径和弧的度数,得到两三角形全等,对应边相等.由三角形相似,对应线段成比例,得到线段乘积的形式,结合图形计算求值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知⊙O的半径为4,A为线段PO的中点,当OP=10时,点A与⊙O的位置关系为( )
| A、在圆上 | B、在圆外 | C、在圆内 | D、不确定 |

 点A、点B重合).连接AC、BC,分别与⊙M相交于点D、点E,连接DE.若AB=2
点A、点B重合).连接AC、BC,分别与⊙M相交于点D、点E,连接DE.若AB=2