Question

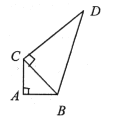
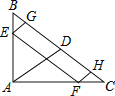
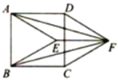
【题目】如图，点E，F分别是正方形ABCD内部、外部的点，四边形ADFE与四边形BCFE均为菱形，连接AF，BF.有如下四个结论：①；②；③EF垂直平分DC；④；其中正确的是（ ）

A.①②④B.①②③C.①③④D.①③

Answer 1

【答案】D

【解析】

根据菱形和正方形的性质，即可得到；由△DCF是等边三角形，得到∠FDC=60°，则；由△CDF是等边三角形，AD⊥CD，AD∥EF，即可得到EF垂直平分DC；延长FE，交AB于点G，则，，由，即可判断.

解：根据题意，在正方形ABCD，菱形ADFE，菱形BCFE中，

∴，故①正确；

∵，

∴△ABE是等边三角形，△DCF是等边三角形，

∴∠AEB=60°，∠FDC=60°

∴∠ADF=90°+60°=150°，

∴，故②错误；

∵AD⊥CD，AD∥EF，

∴EF⊥CD，

∵△DCF是等边三角形，

∴EF垂直平分DC；故③正确；

延长FE，交AB于点G，

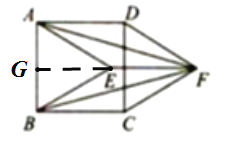
∵EF⊥CD，AB∥CD，

∴EF⊥AB，

∴，，

∵，

∴，故④错误；

∴正确的结论有：①③.

故选择：D.