Question

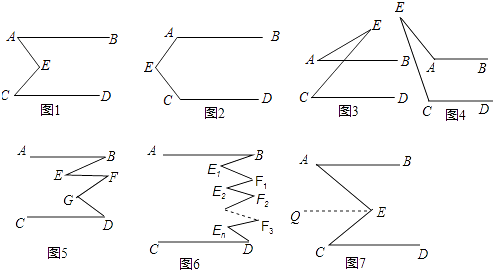
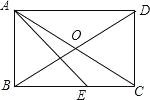
【题目】如图，在矩形ABCD中，AE平分∠BAD交BC于点E，CE=1，∠CAE=15°，则BE等于

Answer 1

【答案】

【解析】

试题分析：由矩形ABCD，得到OA=OB，根据AE平分∠BAD，得到等边三角形OA=OB和△ABE是等腰直角三角形，求出∠BAO，最后用勾股定理计算即可．

∵四边形ABCD是矩形， ∴AD∥BC，AC=BD，OA=OC，OB=OD，∠BAD=90°， ∴OA=OB，∠DAE=∠AEB，∵AE平分∠BAD， ∴∠BAE=∠DAE=45°=∠AEB， ∴AB=BE， ∵∠CAE=15°，

∴∠DAC=45°﹣15°=30°， ∠BAC=60°， ∴△BAO是等边三角形， ∴AB=OB，∠BAO=60°，

在RT△ABC中，BC=AB+CE=AB+1， ∴tan∠BAC===tan60°=， ∴AB=，

∴BE=AB=，