题目内容
【题目】已知:如图,在ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G. 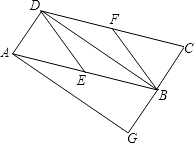
(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴∠4=∠C,AD=CB,AB=CD.
∵点E、F分别是AB、CD的中点,
∴AE= ![]() AB,CF=
AB,CF= ![]() CD.
CD.
∴AE=CF.
在△AED和△CBF中,
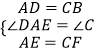 ,
,
∴△ADE≌△CBF(SAS)
(2)解:当四边形BEDF是菱形时,四边形AGBD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AG∥BD,
∴四边形AGBD是平行四边形.
∵四边形BEDF是菱形,
∴DE=BE.
∵AE=BE,
∴AE=BE=DE.
∴∠1=∠2,∠3=∠4.
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°.
∴∠2+∠3=90°.
即∠ADB=90°.
∴四边形AGBD是矩形.
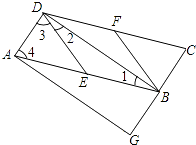
【解析】(1)在证明全等时常根据已知条件,分析还缺什么条件,然后用(SAS,ASA,SSS)来证明全等;(2)先由菱形的性质得出AE=BE=DE,再通过角之间的关系求出∠2+∠3=90°即∠ADB=90°,所以判定四边形AGBD是矩形.
【考点精析】根据题目的已知条件,利用平行四边形的性质和菱形的性质的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目