Question

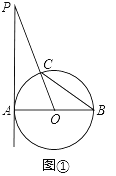
【题目】如图，AB是⊙O的直径，PA切⊙O于A，OP交⊙O于C，连接BC．

（Ⅰ）如图①，若∠P=20°，求∠BCO的度数；

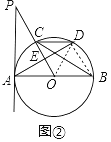
（Ⅱ）如图②，过A作弦AD⊥OP于E，连接DC，若OE= CD，求∠P的度数．

Answer 1

【答案】（Ⅰ）35°（Ⅱ）30°

【解析】

（1）由PA是⊙O的切线，推出OA⊥AP，推出∠AOC=90°-20°=70°，由∠B= ∠AOC=35°，OB=OC，即可推出∠B=∠OCB=35°；
（2）如图2中，连接BD、OD．只要证明 = = ，即可推出∠AOC=∠COD=∠BOD=60°，由PA是⊙O的切线，推出∠PAO=90°，推出∠P=30°；

（Ⅰ）如图1中，

∵PA是⊙O的切线，

∴OA⊥AP，

∴∠PAO=90°，∵∠P=20°，

∴∠AOC=90°﹣20°=70°，

∴∠B= ∠AOC=35°，

∵OB=OC，

∴∠B=∠OCB=35°，

∴∠BCO=35°．

（Ⅱ）如图2中，连接BD、OD．

∵AD⊥OP于E，

∴AE=ED， = ，

∵AE=ED，OA=OB，

∴OE= DB，

∵OE= CD，

∴CD=DB，

∴ = ，

∴ = = ，

∴∠AOC=∠COD=∠BOD=60°，

∵PA是⊙O的切线，

∴∠PAO=90°，

∴∠P=30°