题目内容
【题目】如图,P是半径为![]() cm的⊙O外一点,PA,PB分别和⊙O切于点A,B,PA=PB=3cm,∠APB=60°,C是弧AB上一点,过C作⊙O的切线交PA,PB于点D,E.
cm的⊙O外一点,PA,PB分别和⊙O切于点A,B,PA=PB=3cm,∠APB=60°,C是弧AB上一点,过C作⊙O的切线交PA,PB于点D,E.
(1)求△PDE的周长;
(2)若DE=![]() cm,求图中阴影部分的面积.
cm,求图中阴影部分的面积.

【答案】(1)6cm;
(2)(4﹣π)cm2 .
【解析】试题分析:(1)根据切线长定理得PA=PB=3cm,CE=BE,AD=DC,由三角形周长定义得△PDE的周长=PE+DE+PD,然后利用等线段可得△PDE的周长=PA+PB=6cm;
(2)连接OB、OA、OE,OD,如图,根据切线的性质得∠OBP=∠OPA=90°,再根据四边形内角和计算出∠BOA=120°,利用切线长定理得BE=CE,DC=DA,则根据三角形面积公式得到S△OCE=S△OBE,S△OCD=S△ODA,所以S五边AOBED=2S△ODE=4,然后根据扇形面积公式和图中阴影部分的面积=S五边AOBED-S扇形AOB进行计算.
试题解析:(1)∵PA、PB、DE是⊙O的切线,
∴PA=PB=3cm,CE=BE,AD=DC,
∴△PDE的周长=PE+DE+PD=PE+CE+CD+PD
=PE+BE+AD+PD
=PA+PB
=3cm+3cm
=6cm;
(2)连接OB、OA、OE,OD,如图,
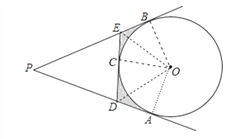
∵PA、PB、OC是⊙O的切线,
∴OB⊥PB,OA⊥PA,OC⊥DE,
∴∠OBP=∠OPA=90°,
∵∠APB=60°,
∴∠BOA=120°,
∵BE=CE,DC=DA,
∴S△OCE=S△OBE,S△OCD=S△ODA ,
∴S五边AOBED=2S△ODE=2×![]() ×
×![]() ×
×![]() =4,
=4,
∴图中阴影部分的面积=S五边AOBED﹣S扇形AOB=4﹣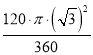 =(4﹣π)cm2.
=(4﹣π)cm2.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目

