Question

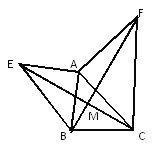
【题目】如图，AC=BC，DC=EC，∠ACB=∠ECD=90°，且∠EBD=38°，则∠AEB=________.

Answer 1

【答案】128°

【解析】

先证明△BDC≌△AEC，进而得到角的关系，再由∠EBD的度数进行转化，最后利用三角形的内角和即可得到答案．

解：
∵∠ACB＝∠ECD＝90°，
∴∠BCD＝∠ACE，
在△BDC和△AEC中，
∵AC＝BC，∠BCD＝∠ACE，DC＝EC，
∴△BDC≌△AEC（SAS），
∴∠DBC＝∠EAC，
∵∠EBD＝∠DBC＋∠EBC＝38°，
∴∠EAC＋∠EBC＝38°，
∴∠ABE＋∠EAB＝90°－38°＝52°，
∴∠AEB＝180°－（∠ABE＋∠EAB）＝180°－52°＝128°，
故答案为：128°．