题目内容
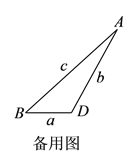
【题目】(1)如图(1),已知任意三角形ABC,过点C作DE∥AB;
①求证:∠DCA=∠A; ②求证:∠A+∠B+∠ACB=180°;
(2)如图(2),求证:∠AGF=∠AEF+∠F;
(3)如图(3),AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=150°,求∠F.

【答案】(1)证明见解析;(2)证明见解析(3)29.5°.
【解析】分析:(1)①根据“两直线平行,内错角相等”可证明;②结合①的证明,转化为平角的意义证明三角形的内角和;
(2)根据平角的意义和三角形的内角和,等量代换即可;
(3)先根据两直线平行,内错角相等,同旁内角互补,求得∠AED和∠DEB的度数,再根据平角的意义和角平分线的性质求得∠DEF的度数,结合(2)的结论可求解.
详解:证明:(1)①∵DE∥BC,∴∠DCA=∠A;
②如图1所示,在△ABC中,∵DE∥BC,
∴∠B=∠ECA,∠DCA=∠A(内错角相等).
∵∠ECA+∠BCA+∠DCA=180°,
∴∠A+∠B+∠C=180°.
即三角形的内角和为180°;
(2)∵∠AGF+∠FGE=180°,
由(1)知,∠GEF+∠F+∠FGE=180°,
∴∠AGF=∠AEF+∠F;
(3)∵AB∥CD,∠CDE=119°,
∴∠DEB=119°,∠AED=61°,
∵GF交∠DEB的平分线EF于点F,
∴∠DEF=59.5°,
∴∠AEF=120.5°,
∵∠AGF=150°,
∵∠AGF=∠AEF+∠F,
∴∠F=150°﹣120.5°=29.5°.

练习册系列答案
相关题目