题目内容
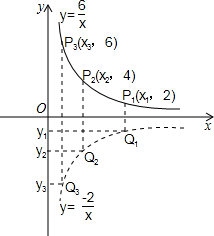 反比例函数y=
反比例函数y=| -2 |
| x |
| 6 |
| x |
| 6 |
| x |
| -2 |
| x |
分析:由图象可知Pn的纵坐标为2n(n为正整数),代入y=
中,得xn=
,而两条双曲线上各点对应的横坐标分别相等,把xn=
代入y=
中,得yn=-
n,按照纵坐标变化的规律可求y2010的值.
| 6 |
| x |
| 3 |
| n |
| 3 |
| n |
| -2 |
| x |
| 2 |
| 3 |
解答:解:依题意,得Pn的纵坐标为2n(n为正整数),
把y=2n代入y=
中,得xn=
,
∵两条双曲线上各点对应的横坐标分别相等,
把xn=
代入y=
中,得yn=-
n,
∴当n=2010时,y2010=-1340.
故本题答案为:-1340.
把y=2n代入y=
| 6 |
| x |
| 3 |
| n |
∵两条双曲线上各点对应的横坐标分别相等,
把xn=
| 3 |
| n |
| -2 |
| x |
| 2 |
| 3 |
∴当n=2010时,y2010=-1340.
故本题答案为:-1340.
点评:本题考查了反比例函数图象上点的坐标特点.关键是判断双曲线y=
上点的纵坐标规律,根据两条双曲线对应点横坐标相等进行规律的推导.
| 6 |
| x |

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
设A(x1,y1)、B(x2,y2)是反比例函数y=
图象上的任意两点,且y1<y2,则x1,x2可能满足的关系是( )
| -2 |
| x |
| A、x1>x2>0 |
| B、x1<0<x2 |
| C、x2<0<x1 |
| D、x2<x1<0 |
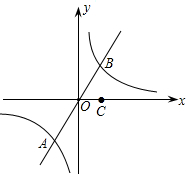 若一次函数y=2x和反比例函数y=
若一次函数y=2x和反比例函数y=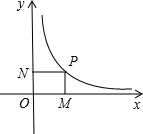 已知,如图,反比例函数
已知,如图,反比例函数