Question

【题目】如图1，将一副直角三角板放在同一条直线AB上，其中∠ONM＝30°，∠OCD＝45°

（1）观察猜想

将图1中的三角尺OCD沿AB的方向平移至图②的位置，使得点O与点N重合，CD与MN相交于点E，则∠CEN＝　 度．

（2）操作探究

将图1中的三角尺OCD绕点O按顺时针方向旋转，使一边OD在∠MON的内部，如图3，且OD恰好平分∠MON，CD与NM相交于点E，求∠CEN的度数；

（3）深化拓展

将图1中的三角尺OCD绕点O按沿顺时针方向旋转一周，在旋转的过程中，若边CD恰好与边MN平行，请你求出此时旋转的角度．

Answer 1

【答案】（1）105°；（2）∠CEN＝150°；（3）75或255．

【解析】

（1）根据三角形的内角和定理列式计算即可得解；

（2）由OD平分∠MON，得∠DON＝ ∠MPN＝45°，则∠DON＝∠D＝45°，可得CD∥AB， 由两直线平行，同旁内角互补，可得出∠CEN＝150°；

（3）分当CD在AB上方及当CD在AB的下方两种情况进行讨论，画出具体图形，进行计算即可。

（1）∵∠ECN＝45°，∠ENC＝30°，

∴∠CEN＝180-75=105°．故答案为：105°．

（2）∵OD平分∠MON，

∴∠DON＝∠MPN＝×90°＝45°，

∴∠DON＝∠D＝45°，

∴CD∥AB，

∴∠CEN＝180°﹣∠MNO＝180°﹣30°＝150°；

（3）如图1，CD在AB上方时，设OM与CD相交于F，

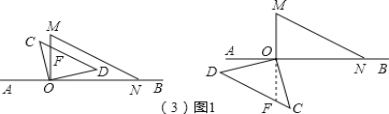
∵CD∥MN，

∴∠OFD＝∠M＝60°，

在△ODF中，∠MOD＝180°﹣∠D﹣∠OFD，

＝180°﹣45°﹣60°，

＝75°，

当CD在AB的下方时，设直线OM与CD相交于F，

∵CD∥MN，

∴∠DFO＝∠M＝60°，

在△DOF中，∠DOF＝180°﹣∠D﹣∠DFO＝180°﹣45°﹣60°＝75°，

∴旋转角为75°+180°＝255°，

综上所述，旋转的角度为75°或255°时，边CD恰好与边MN平行．

故答案为：75或255．