��Ŀ����
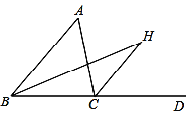
����Ŀ����ͼ����ABC�ı�BC��ֱ��l�ϣ�AC��BC����AC��BC����EFP�ı�FPҲ��ֱ��l�ϣ���EF���AC�غϣ���EF��FP.
(1)��ͼ���У�����ͨ���۲졢���������룬д��AB��AP�������������ϵ��λ�ù�ϵ��
(2)����EFP��ֱ��l����ƽ�Ƶ�ͼ�ڵ�λ��ʱ��EP��AC�ڵ�Q������AP��BQ�����벢д��BQ��AP�������������ϵ��λ�ù�ϵ����֤����IJ��룻
(3)����EFP��ֱ��l����ƽ�Ƶ�ͼ�۵�λ��ʱ��EP���ӳ��߽�AC���ӳ����ڵ�Q������AP��BQ������Ϊ(2)���������BQ��AP��������ϵ��λ�ù�ϵ��������������������֤����������������˵�����ɣ�

���𰸡�(1)AB��AP��AB��AP (2)BQ��AP��BQ��AP (3)����
��������
��1������ͼ�ξͿ��Բ�������ۣ���2��Ҫ֤BQ=AP������ת��Ϊ֤��Rt��BCQ��Rt��ACP��Ҫ֤��BQ��AP������֤����QMA=90����ֻҪ֤����1=��2����3=��4����1+��3=90������֤������3����ȣ�2����֤���Ϳ��Եõ��������Գ�����
(1)AB��AP��AB��AP
֤������AC��BC��AC=BC��
���ABCΪ����ֱ�������Σ�
���BAC=��ABC=![]() ��180�㩁��ACB��=45�㣬
��180�㩁��ACB��=45�㣬
�֡ߡ�ABC����EFPȫ�ȣ�
ͬ����֤��PEF=45�㣬
���BAP=45��+45��=90�㣬
��AB=AP��AB��AP��
��2��BQ=AP��BQ��AP��
֤����������֪����EF=FP��EF��FP��
���EPF=45�㣮
�֡�AC��BC��
���CQP=��CPQ=45�㣮
��CQ=CP��
����Rt��BCQ��Rt��ACP��
BC=AC����BCQ=��ACP=90�㣬CQ=CP��
���BCQ�ա�ACP��SAS����
��BQ=AP��
����ͼ���ӳ�BQ��AP�ڵ�M��
��Rt��BCQ��Rt��ACP��
���1=��2��
����Rt��BCQ�У���1+��3=90�����֡�3=��4��
���2+��4=��1+��3=90�㣮
���QMA=90�㣮
��BQ��AP��
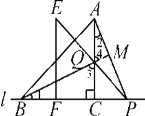
(3)������֤�����ߡ�EPF��45�㣬���CPQ��45��.�֡�AC��BC�����CQP����CPQ��45�㣬��CQ��CP.��SAS��֤��BCQ�ա�ACP����BQ��AP.�ӳ�QB��AP�ڵ�N�����PBN����CBQ.�ߡ�BCQ�ա�ACP�����BQC����APC.��Rt��BCQ�У���BQC����CBQ��90�㣬���APC����PBN��90�㣬���PNB��90�㣬��BQ��AP

 Ӣ��СӢ������Ĭдϵ�д�
Ӣ��СӢ������Ĭдϵ�д� �����ҵ���������ͯ������ϵ�д�
�����ҵ���������ͯ������ϵ�д�