题目内容
已知二次函数y=x2+kx+
k-
.
(1)求证:不论k为任何实数,该函数的图象与x轴必有两个交点;
(2)若该二次函数的图象与x轴的两个交点在点A(1,0)的两侧,且关于x的一元二次方程k2x2+(2k+3)x+1=0有两个不相等的实数根,求k的整数值;
(3)在(2)的条件下,关于x的另一方程x2+2(a+k)x+2a-k2+6k-4=0 有大于0且小于3的实数根,求a的整数值.
| 1 |
| 2 |
| 7 |
| 2 |
(1)求证:不论k为任何实数,该函数的图象与x轴必有两个交点;
(2)若该二次函数的图象与x轴的两个交点在点A(1,0)的两侧,且关于x的一元二次方程k2x2+(2k+3)x+1=0有两个不相等的实数根,求k的整数值;
(3)在(2)的条件下,关于x的另一方程x2+2(a+k)x+2a-k2+6k-4=0 有大于0且小于3的实数根,求a的整数值.
(1)证明:x2+kx+
k-
=0,
△1=b2-4ac=k2-4(
k-
)
=k2-2k+14
=k2-2k+1+13
=(k-1)2+13>0,
∴不论k为任何实数,该函数的图象与x轴必有两个交点;
(2)∵二次函数y=x2+kx+
k-
的图象与x轴的两个交点在点(1,0)的两侧,且二次函数开口向上,
∴当x=1时,函数值y<0,
即1+k+
k-
<0,
解得:k<
,
∵关于x的一元二次方程k2x2+(2k+3)x+1=0有两个不相等的实数根,
∴k≠0且△2=b2-4ac=(2k+3)2-4k2=4k2+12k+9-4k2=12k+9>0,
∴k>-
且k≠0,
∴-
<k<
且k≠0,
∴k=1;
(3)由(2)可知:k=1,
∴x2+2(a+1)x+2a+1=0,
解得x1=-1,x2=-2a-1,
根据题意,0<-2a-1<3,
∴-2<a<-
,
∴a的整数值为-1.
| 1 |
| 2 |
| 7 |
| 2 |
△1=b2-4ac=k2-4(
| 1 |
| 2 |
| 7 |
| 2 |
=k2-2k+14
=k2-2k+1+13
=(k-1)2+13>0,
∴不论k为任何实数,该函数的图象与x轴必有两个交点;
(2)∵二次函数y=x2+kx+
| 1 |
| 2 |
| 7 |
| 2 |
∴当x=1时,函数值y<0,
即1+k+
| 1 |
| 2 |
| 7 |
| 2 |
解得:k<
| 5 |
| 3 |
∵关于x的一元二次方程k2x2+(2k+3)x+1=0有两个不相等的实数根,
∴k≠0且△2=b2-4ac=(2k+3)2-4k2=4k2+12k+9-4k2=12k+9>0,
∴k>-
| 3 |
| 4 |
∴-
| 3 |
| 4 |
| 5 |
| 3 |
∴k=1;
(3)由(2)可知:k=1,
∴x2+2(a+1)x+2a+1=0,
解得x1=-1,x2=-2a-1,
根据题意,0<-2a-1<3,
∴-2<a<-
| 1 |
| 2 |
∴a的整数值为-1.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
已知二次函数y=x2+(2a+1)x+a2-1的最小值为0,则a的值是( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
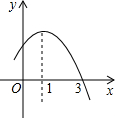 已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为( )
已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为( )| A、x1=1,x2=3 | B、x1=0,x2=3 | C、x1=-1,x2=1 | D、x1=-1,x2=3 |
 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).