题目内容
【题目】在直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点P分别作x轴,y轴的垂线,与坐标轴围成矩形OAPB的周长与面积相等,则点P是和谐点.
(1)点M(3,2) 和谐点(填“是”或“不是”);
(2)若点P(a,6)是和谐点,a的值为
(3)若(2)中和谐点P(a,6)在y=﹣4x+m上,m= 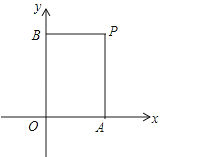
【答案】不是;±3;18或﹣6
【解析】解:(1)∵点M(3,2),
∴矩形OAPB的周长=2(3+2)=10,
面积=3×2=6,
∵10≠6,
∴则点M(3,2)不是和谐点;
故答案为:不是;
(2)根据题意得:2(|a|+6)=6|a|,
解得:a=±3;
故答案为:±3;
(3)∵点P(a,6)在直线y=﹣4x+m上,
∴﹣4a+m=6,即m=4a+6,
当a=3时,m=18;当a=﹣3时,m=﹣6,
∴m的值为18或﹣6.
(1)根据和谐点的定义求出矩形的周长与面积,然后即可判断;
(2)根据题意列出方程,求出方程的解得到a的值即可;
(3)利用一次函数图象上点的坐标特征得到﹣4a+m=6,即m=4a+6,然后把a的值分别代入可计算出对应的m的值.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目