题目内容
【题目】在平面直角坐标系中,已知△ABC顶点坐标分别为A(0,3),B(1,1),C(﹣3,﹣1),△DEF与△ABC关于y轴对称,且A,B,C依次对应D,E,F,
(1)请写出D,E,F的坐标.
(2)在平面直角坐标系中画出△ABC和△DEF.
(3)经过计算△DEF各边长度,发现DE、EF、FD满足什么关系式,写出关系式.
(4)求△DEF的面积.
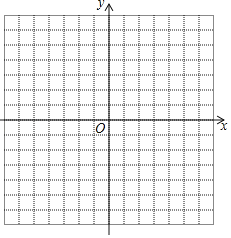
【答案】(1)D(0,3),E(-1,1),F(3,-1);(2)见解析;(3)DE2+EF2=DF2;(4)S△DEF=5.
【解析】
(1)依据△DEF与△ABC关于y轴对称,且A,B,C依次对应D,E,F,即可得到D(0,3),E(1,1),F(3,1);
(2)依据A(0,3),B(1,1),C(3,1),D(0,3),E(1,1),F(3,1),即可得到△ABC和△DEF;
(3)由勾股定理可得,DE2=5,EF2=20,DF2=25,即可得到DE、EF、FD满足:DE2+EF2=DF2;
(4)依据割补法进行计算,即可得到△DEF的面积.
(1)∵△DEF与△ABC关于y轴对称,且A,B,C依次对应D,E,F,
∴D(0,3),E(1,1),F(3,1);
(2)如图所示:△ABC和△DEF即为所求.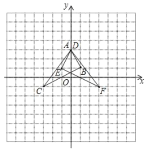
(3)由勾股定理可得,DE2=5,EF2=20,DF2=25,
∴DE、EF、FD满足:DE2+EF2=DF2;
(4)S△DEF=4×4![]() ×1×2
×1×2![]() ×2×4
×2×4![]() ×3×4=16146=5.
×3×4=16146=5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目