题目内容
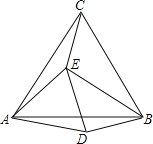
【题目】如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H,AE=CF,BE=EG.

(1)求证:EF∥AC;
(2)求∠BEF大小;
【答案】(1)、证明过程见解析;(2)、60°.
【解析】试题分析:(1)、根据正方形的性质得出AD∥BF,结合AE=CF可得四边形ACFE是平行四边形,从而得出EF∥AC;(2)、连接BG,根据EF∥AC可得∠F=∠ACB=45°,根据∠GCF=90°可得∠CGF=∠F=45°可得CG=CF,根据AE=CF可得AE=CG,从而得出△BAE≌△BCG,即BE=EG,得出△BEG为等边三角形,得出∠BEF的度数.
试题解析:(1)、∵四边形ABCD是正方形 ∴AD∥BF ∵AE="CF" ∴四边形ACFE是平行四边形 ∴EF∥AC
(2)、连接BG ∵EF∥AC, ∴∠F=∠ACB=45°, ∵∠GCF=90°, ∴∠CGF=∠F=45°, ∴CG=CF,
∵AE=CF, ∴AE=CG, ∴△BAE≌△BCG(SAS) ∴BE=BG, ∵BE=EG, ∴△BEG是等边三角形,
∴∠BEF=60°

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目