Question

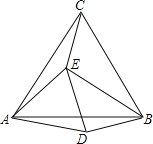
【题目】如图，等边△ABC和等边△ADE中，AB=2，AD=2，连CE，BE，当∠AEC=150°时，则BE= ．

Answer 1

【答案】4

【解析】

试题分析：如作CM⊥AE于M，设CM=a，在RT△ACM利用勾股定理求出a，再求出CE，由△CAE≌△BAD，得到EC=BD，在RT△EBD中利用勾股定理即可求出BE．

解：如作CM⊥AE于M，设CM=a，

∵△ABC、△ADE都是等边三角形，

∴AC=AB=2，AE=AD=DE=2，∠CAB=∠EAD=∠EDA=60°，

∴∠CAE=∠BAD，

在△CAE和△BAD中，

，

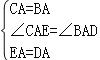∴△CAE≌△BAD，

∴EC=BD，∴∠AEC=∠ADB=150°，

∴∠EDB=90°，

∵∠AEC=150°，

∴∠CEM=180°﹣∠AEC=30°，

∴EM=a，

在RT△ACM中，∵AC2=CM2+AM2，

∴28=a2+（2+a）2

a=1（或﹣4舍弃），

∴EC=BD=2CM=2，

在RT△EBD中，∵DE=2，BD=2，

∴EB===4．

故答案为4．