Question

【题目】如图，抛物线的顶点坐标为，并且与轴交于点，与轴交于、两点．

（）求抛物线的表达式．

（）如图，设抛物线的对称轴与直线交于点，点为直线上一动点，过点作轴的平行线，与抛物线交于点，问是否存在点，使得以、、为顶点的三角形与相似．若存在，求出点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）或或或.

【解析】试题分析：（1）设抛物线的表达式为y=a（x-2）2-1（a≠0），将点C的坐标代入即可得出答案；（2）由直线BC的解析式知，∠OBC=∠OCB=45°．又由题意知∠EFD=∠COB=90°，所以只有△EFD∽△COB，根据这种情况求点E的坐标即可．

试题解析：

（）该抛物线的顶点坐标为，所以该抛物线的解析式为，又该抛物线过点，代入得：

，解得，故该抛物线的解析式为+3．

（）假设存在点E，使得以D、E、F为顶点的三角形与△BCO相似．

由（1）知，该抛物线的解析式是y=x2-4x+3，即y=（x-1）（x-3），

∴该抛物线与x轴的交点坐标分别是A（1，0），B（3，0）．

∵C（0，3），

∴易求直线BC的解析式为：y=-x+3．

∴∠OBC=∠OCB=45°．

又∵点D是对称轴上的一点，

∴D（2，1）．

如图，连接DF．

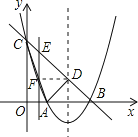
∵EF∥y轴，

∴只有∠EFD=∠COB=90°．

∵以D、E、F为顶点的三角形与△BCO相似，

∴∠DEF=∠FDE=45°，

∴只有△EFD∽△COB．

设E（x，-x+3），则F（x，1），

∴1=x2-4x+3，

解得x=2± ，

当x=2+时，y=-x+3=1-；

当x=2-时，y=-x+3=1+；

∴E1（2-，1+）、E2（2+，1-）．

∠EDF=90°；易知，直线AD：y=x-1，联立抛物线的解析式有：

x2-4x+3=x-1，解得 x1=1、x2=4；

当x=1时，y=-x+3=2；

当x=4时，y=-x+3=-1；

∴E3（1，2）、E4（4，-1）．

∴综上，点E的坐标为（2-，1+）或（2+，1-）或（1，2）或（4，-1）．