题目内容
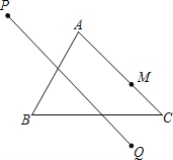
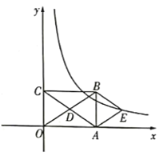
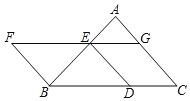
【题目】如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.
(1)求证:四边形BDEF为平行四边形;
(2)当∠C=30°,![]() 时,求D,F两点间的距离.
时,求D,F两点间的距离.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据等腰△ABC的性质,结合EG∥BC,DE∥AC 的性质,等角代换可以证得∠F=∠DEG,得出BF∥DE即可;
(2)作EN⊥BD于N,作FM⊥BD于M,连接DF ,利用(1)中的结论,结合含30°的直角三角形的性质可以得出Rt△FMD中FM、DM的长度,结合勾股定理即可求得.
(1)∵△ABC是等腰三角形,
∴∠ABC=∠C,
∵EG∥BC,DE∥AC,
∴∠AEG=∠ABC=∠C,四边形CDEG是平行四边形,
∴∠DEG=∠C,
∵BE=BF,
∴∠BFE=∠BEF=∠AEG=∠ABC,
∴∠F=∠DEG,
∴BF∥DE,EF∥BD
∴四边形BDEF为平行四边形;
(2)解:作EN⊥BD于N,作FM⊥BD于M,连接DF,如图所示:
∵∠C=30°,AB=AC,四边形BDEF为平行四边形,
∴∠ABC=∠BFE=∠BEF=∠NBE=∠C=30°,
∴△BDE、△BEF是等腰三角形,
∴BE=DE=BF,
∵EN⊥BD,
∴BN=![]() BD=
BD=![]() ,
,
∴EN=![]() =1,
=1,
∴BF=BE=2EN=2,
∴FM=![]() BF=1,
BF=1,
∴BM=![]() FM=
FM=![]() ,
,
∴DM=BM+BD=3![]() ,
,
由勾股定理得:DF=![]() =
=![]() =
=![]() ,
,
即D,F两点间的距离为![]() ,
,
故答案为:![]() .
.


练习册系列答案
相关题目