Question

【题目】抛物线y＝﹣x交x轴于点A，点B（6，n）为抛物线上一点．

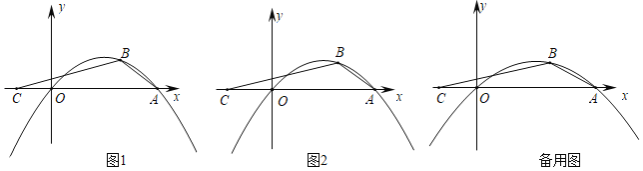
（1）求m与n之间的函数关系；

（2）如图，点C（﹣n，0）在x轴上，且∠BAC＝2∠ACB，求m的值；

（3）在（2）的条件下，P为直线BC上方抛物线上一点，过点P作PD∥AB交x轴于点D，DE⊥BC交OP于点E，，求点P坐标．

Answer 1

【答案】(1)n＝m；(2)3；(3)P（4，3）

【解析】

（1）将点B（6，n）代入y＝﹣x，得到n＝m；

（2）过点B作BG⊥x轴，作∠BAC的角平分线交BG于点M，过点M作MN⊥AB，求出A（n+6，0），B（6，n），在Rt△ABC中，tan∠BAO＝，可求得tan∠MAG＝tan∠BAC＝，则有＝，即可求出n＝m＝3；

（3）由（2）可得y＝﹣x2+x，设P（t，﹣t2+t），由可得＝，所以求出E（t，﹣t2+2t），分别求出BC的解析式为y＝x+1，DE的解析式为y＝﹣3x﹣t2+t，即可求D（﹣t2+t，0），又由DP∥AB，得到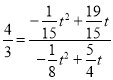，所以t＝4即可求P的坐标．

（1）将点B（6，n）代入y＝﹣x，得：

n=，

化简得：n＝m；

（2）过点B作BG⊥x轴，作∠BAC的角平分线交BG于点M，过点M作MN⊥AB，

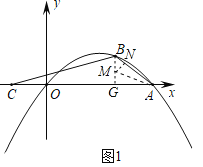
∵A（n+6，0），B（6，n），

∴AG＝n，

在Rt△ABG中，tan∠BAO＝，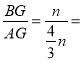

∵MN⊥AB，MG⊥OA，

∴MN＝MG，

∵在Rt△MNB和Rt△AGB中，∠B为相等的角，

∴Rt△MNB∽Rt△AGB

∴，

设BN=3x,MN=4x，则BM＝5x,

∵BG-MB=MG，MG=MN，

∴n-5x=4x，解得x=，

∴MG＝MN＝，

∴tan∠MAG＝，

∵∠BAC＝2∠ACB，

∴tan∠BAC＝，

∵C（﹣n，0），

∴＝，

∴n＝3，

∴m＝3；

（3）如图所示：

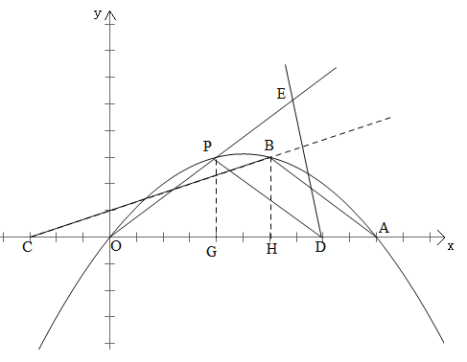
由（2）可得y＝﹣x2+x，

设P（t，﹣t2+t），

∵，

∴＝，

∴E（t，﹣t2+2t），

∵B（6，3），A（10，0），C（﹣3，0），

∴BC的解析式为y＝x+1，

∵BC⊥DE，

∴设直线DE的解析式为y=-3x+k，

把E（t，﹣t2+2t）代入y=-3x+k中得：k=﹣t2+t，

∴DE的解析式为y＝﹣3x﹣t2+t，

∴D（﹣t2+t，0），

∵DP∥AB，

∴ ，

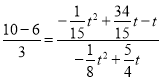∴ 即，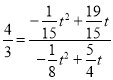

∴解方程得：t＝4或t＝0（增根，舍去），

∵P点在BC直线上方，

∴t＞0，

∴t＝4符合题意，

∴P（4，3）．