��Ŀ����
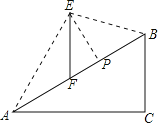
����Ŀ����ͼ������ABCD�У�AB=13��BC=50��BC���ϵĸ�Ϊ12����P�ӵ�B��������B��A��D��A�˶�����B��A�˶�ʱ���ٶ�Ϊÿ��13����λ���ȣ���A��D��A�˶�ʱ���ٶ�Ϊÿ��8����λ���ȣ���Q�ӵ� B������BC�����˶����ٶ�Ϊÿ��5����λ���ȣ�P��Q����ͬʱ����������Q�����Cʱ��P��Q����ͬʱֹͣ�˶������P���˶�ʱ��Ϊt���룩������PQ��
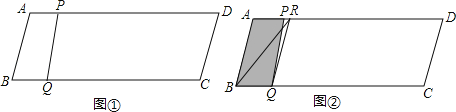
��1������P��A��D��A�˶�ʱ����AP�ij����ú�t�Ĵ���ʽ��ʾ����
��2������AQ���ڵ�P��B��A��D�˶������У�����P���B����A���غ�ʱ������APQ�����ΪS����S��t֮��ĺ�����ϵʽ��
��3������Q��QR��AB����AD�ڵ�R������BR����ͼ�����ڵ�P��B��A��D�˶������У����߶�PQɨ����ͼ�Σ���Ӱ���֣����߶�BR�ֳ������ȵ�������ʱt��ֵ��
��4�����C��D����ֱ��PQ�ĶԳƵ�ֱ�ΪC�䡢D�䣬ֱ��д��C��D����BCʱt��ֵ��
���𰸡���1��108��8t��
��2��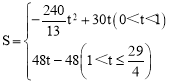 ��
��
��3����t=1��![]() ʱ���߶�PQɨ����ͼ�Σ���Ӱ���֣����߶�BR�ֳ������ȵ���������
ʱ���߶�PQɨ����ͼ�Σ���Ӱ���֣����߶�BR�ֳ������ȵ���������
��4����t=7��t=![]() ��t=
��t=![]() ʱ����C��D����ֱ��PQ�ĶԳƵ�ֱ�ΪC�䡢D�䣬��C��D����BC��
ʱ����C��D����ֱ��PQ�ĶԳƵ�ֱ�ΪC�䡢D�䣬��C��D����BC��
��������
������1�����������������P��A��D�˶�ʱ������P��D��A�˶�ʱ�ֱ���Ա�ʾ��AP��ֵ��
����P��A��D�˶�ʱ��AP=8��t��1��=8t��8��
����P��D��A�˶�ʱ��AP=50��2��8��t��1��=108��8t��
��2��������������0��t��1ʱ����1��t��![]() ʱ�����������ε������ʽ�ֱ����S��t�ĺ�����ϵʽ��
ʱ�����������ε������ʽ�ֱ����S��t�ĺ�����ϵʽ��
����P���A�غ�ʱ��BP=AB��t=1��
����P���D�غ�ʱ��AP=AD��8t��8=50��t=![]() ��
��
��0��t��1ʱ����ͼ��

������Q��QE��AB�ڵ�E��
S��ABQ=![]() ��
��
��![]() ��
��
��![]() ��
��
��S=![]() ��
��
��1��t��![]() ʱ����ͼ��
ʱ����ͼ��
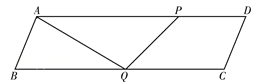
S=![]() ��
��
���������� 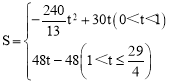 ��
��
��3��������������0��t��1ʱ����1��t��![]() ʱ����
ʱ����![]() ��t��
��t��![]() ʱ�����������ε������Ƚ������������⼴����
ʱ�����������ε������Ƚ������������⼴����
��P���R�غ�ʱ��AP=BQ��8t��8=5t��t=![]() ��
��
��0��t��1ʱ����ͼ��

��S��BPM=S��BQM����PM=QM��
��AB��QR��
���PBM=��QRM����BPM=��MQR��
����BPM����RQM��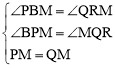 ��
��
���BPM�ա�RQM��AAS������BP=RQ��
��RQ=AB����BP=AB��
��13t=13����ã�t=1��
��1��t��![]() ʱ����ͼ��
ʱ����ͼ��

��BRƽ����Ӱ�����������P���R�غϡ�
��t=![]() ��
��
��![]() ��t��
��t��![]() ʱ����ͼ��
ʱ����ͼ��
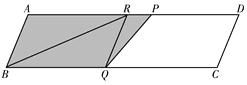
��S��ABR=S��QBR����S��ABR��S�ı���BQPR��
��BR���ܰ��ı���ABQP�ֳ������ȵ������֡�
��4������������
��P��A��D֮���D��A֮����C��D����BC�Ϸ���C��D����BCʱ����ͼ��
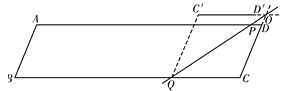
���C��OQ=��OQC��
�ߡ�C��OQ�ա�COQ�����C��OQ=��COQ��
���CQO=��COQ����QC=OC��
��50��5t=50��8��t��1��+13��
��50��5t=8��t��1����50+13��
��ã�t=7��t=![]() ��
��
��P��A��D֮���D��A֮�䣬C��D����BC�·���C��D����BCʱ����ͼ��

ͬ�������ε����ʿ��Եó���OD=PD��
��50��5t+13=50��8��t��1����
��50��5t+13=50����108��8t����
50��5t+13=50��8��t��1���⣻
��50��5t+13=50����108��8t����ã�t=![]() ��
��
������������t=7��t=![]() ��t=
��t=![]() ʱ����C��D����ֱ��PQ�ĶԳƵ�ֱ�ΪC�䡢D�䣬��C��D����BC��
ʱ����C��D����ֱ��PQ�ĶԳƵ�ֱ�ΪC�䡢D�䣬��C��D����BC��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�