Question

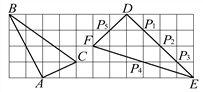
【题目】已知△ABC的三个顶点的坐标分别为A（﹣5，0）、B（﹣2，3）、C（﹣1，0）

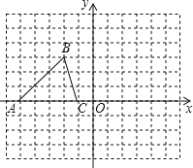
（1）画出△ABC向下平移3个单位的△A1B1C1；

（2）将△A1B1C1绕原点O旋转180°，画出旋转后的△A2B2C2；

（3）在（2）中，线段A1B1 扫过的面积为　 　 ．（设图中小正方的边长为1个单位长度）

Answer 1

【答案】（1）图形见解析；（2）图形见解析；（3）15π.

【解析】

（1）利用网格特点和平移的性质画出、写出A、B、C的对应点A1、B1、C1的坐标，顺次连接，从而得到△A1B1C1；（2）利用网格特点和中心对称的性质画出、写出 A1、B1、C1的对应点A2、B2、C2的坐标，顺次连接，从而得到△A2B2C2；（3）线段A1B1 扫过的面积为以O A1为半径的半圆面积减去以O B1为半径的半圆面积.

解：（1）△A1B1C1见图形；（2）△A2B2C2见图形；

（3）线段A1B1 扫过的面积=(π×OA1 2-π×OB1 2 ) ÷2=π×（34-4）÷2=15π