题目内容
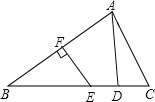
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,点D在AC上,点E在BA的延长线上,BD与CE相交于点F, 且BD=CE.

(1)求证:BF⊥CE.
(2)如图2,连结AF ,证明AF平分∠BFE.
【答案】(1)见解析;(2)见解析
【解析】
(1)由![]() 可得出
可得出![]() ,根据
,根据![]() 、
、![]() 可证出
可证出![]() ,根据全等三角形的性质可得出
,根据全等三角形的性质可得出![]() ,进而可得出
,进而可得出![]() ,再根据
,再根据![]() 结合三角形内角和定理可得出
结合三角形内角和定理可得出![]() ,即
,即![]() ,此题得证.
,此题得证.
(2)过A点作BE、EF垂线段AG、AH,由三角形全等可得AG=AH,从而根据角平分线的判定即可得出结论.
证明:(1)![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,即
,即![]() .
.
(2)如图:过A点作△ABD和△AEC的高 AG、AH,

![]() ,
,
∴![]() ,即
,即![]() ,
,
又∵BD=FC,
∴AH=AG,
∴AF平分∠EBC.

练习册系列答案
相关题目