题目内容
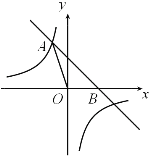
【题目】如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，顶点A，C分别在坐标轴上，顶点B的坐标为，过点D和E的直线分别与AB，BC交于点M，N。
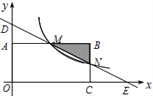
（1）、求直线DE的解析式和点M的坐标；
（2）、若反比例函数y=
的图象经过点M，求该反比例函数的解析式，并通过计算判断点N是否在该函数的图象上；
（3）、若反比例函数的图象与△MNB有公共点，请直接写出m的取值范围。
【答案】（1）、y=-
x+3，M（2，2）；（2）、y=
，在；（3）、4≤m≤8
【解析】试题分析：（1）、已知点D（0，3）和E（6，0），设DE直线解析式为y=ax+b，分别把x=0，y=3和x=6，y=0代入解析式，解得a=-，b=3.求出DE直线解析式；已知DE解析式，M为DE直线上的点，且M在AB上，故M点y值为2. 把y=2代入解得x=2，故M点坐标（2,2）；（2）、把M点坐标代入反比例函数，求得m=4，
已知N在BC上，故N点所对x=4.把x=4代入得y=1，N（4,1），故4×1=4=m，故N在反比例函数上；（3）、若反比例函数（x>0）的图象与△MNB有公共点，M点坐标（2,2），N（4，1），B（4，2）。则在x值范围2≤x≤4时，对应y值范围在1≤y≤2，且m=xy。故m的取值范围为：4≤m≤8
试题解析：（1）、设DE直线解析式为y=ax+b
将（0,3）和（6,0）代入可得：
解得：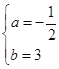
∴函数解析式为y=-x+3
根据题意可得：
点M的纵坐标为2，代入直线y=-x+3可得：x=2
即点M的坐标为（2,2）
（2）、将点M（2,2）代入y=
可得：m=4 即反比例函数的解析式为：y=
将x=4代入反比例函数解析式可得：y=1，即点N在反比例函数图像上.
（3）、∵反比例函数（x>0）的图象与△MNB有公共点，M（2,2），N（4，1），B（4，2）
∴2≤x≤4
则1≤y≤2
∵m=xy
∴4≤m≤8
