Question

【题目】如图，已知AB是⊙O的直径，过点O作弦BC的平行线，交过点A的切线AP于点P，连接AC．

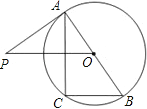
（1）求证：△ABC∽△POA；

（2）若OB=2，OP=，求BC的长．

Answer 1

【答案】（1）证明见解析；（2）BC=．

【解析】

试题分析：（1）由BC∥OP可得∠AOP=∠B，根据直径所对的圆周角为直角可知∠C=90°，再根据切线的性质知∠OAP=90°，从而可证△ABC∽△POA；

（2）根据△ABC∽△POA，和已知边的长可将BC的长求出．

（1）证明：∵BC∥OP

∴∠AOP=∠B

∵AB是直径

∴∠C=90°

∵PA是⊙O的切线，切点为A

∴∠OAP=90°

∴∠C=∠OAP

∴△ABC∽△POA；

（2）解：∵△ABC∽△POA

∴

∵OB=2，PO=

∴OA=2，AB=4

∴

∴BC=8

∴BC=．