题目内容
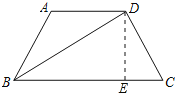
【题目】梯形ABCD中，AD∥BC，AB=DC=2
，∠DBC=30°，∠BDC=90°，求：梯形ABCD的面积．
【答案】9
．
【解析】
试题分析：作DE⊥BCTVE，则∠DEB=90°，由含30°角的直角三角形的性质得出DE=
BD，BC=2DC=4
，求出BD=DC=6，DE=3，由等腰梯形的性质得出∠ABD=∠ADB，得出AD=AB=2，即可求出梯形ABCD的面积．
解：如图所示：
作DE⊥BCTVE，则∠DEB=90°，
∵∠DBC=30°，∠BDC=90°，
∴∠C=60°，DE=BD，BC=2DC=4，BD=DC=6，
∴DE=3，
∵AD∥BC，AB=DC，
∴∠ABC=∠C=60°，∠ADB=∠BDC=30°，
∴∠ABD=30°=∠ADB，
∴AD=AB=2，
∴梯形ABCD的面积=（AD+BC）×DE=
（2+4）×3=9．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
