题目内容
 如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比.
如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比.
分析:设每个小正方形的边长为1,分别求得两个三角形的各边的长,从而求得其三边的对应比例相等可判定两三角形相似,相似比即可求得.
解答:解:设每个小正方形的边长为1,则AB=2,AC=
,BC=
,DE=4,DF=2
,EF=2
.
∵
=
=
=
∴△ABC∽△DEF,(4分)
相似比=
.(6分)
| 2 |
| 10 |
| 2 |
| 10 |
∵
| AB |
| DE |
| AC |
| DF |
| BC |
| EF |
| 1 |
| 2 |
∴△ABC∽△DEF,(4分)
相似比=
| 1 |
| 2 |
点评:此题考查学生对相似三角形的判定方法的理解及运用能力,比较简单.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
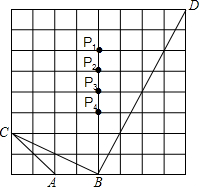 如图,在正方形网格上,若使△ABC∽△PBD,则点P应在( )处.
如图,在正方形网格上,若使△ABC∽△PBD,则点P应在( )处.| A、P1 | B、P2 | C、P3 | D、P4 |
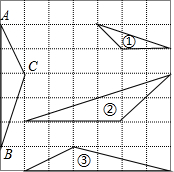 如图,在正方形网格上的三角形①,②,③中,与△ABC相似的三角形有
如图,在正方形网格上的三角形①,②,③中,与△ABC相似的三角形有 如图,在正方形网格上有三个三角形,则与△FDE相似的三角形是
如图,在正方形网格上有三个三角形,则与△FDE相似的三角形是 如图,在正方形网格上有△ABC和△DEF.
如图,在正方形网格上有△ABC和△DEF. 作图计算题.
作图计算题.