题目内容
 如图,在正方形网格上有三个三角形,则与△FDE相似的三角形是
如图,在正方形网格上有三个三角形,则与△FDE相似的三角形是△HGR
△HGR
.分析:根据网格结构,利用勾股定理求出三个三角形的三边,再求出三边的比,然后根据三边对应成比例的两个三角形相似确定.
解答:解:在△FDE中,DF=
=
,DE=2,EF=
=
,
所以,三边之比为
:2:
=1:
:
;
在△ABC中,AC=
=
,AB=6,BC=
=
,
所以,三边之比为
:6:
;
在△HGR中,HG=
=2
,GR=4,HR=
=2
,
所以,三边之比为2
:4:2
=1:
:
;
所以,与△FDE相似的三角形是△HGR.
故答案为:△HGR.
| 12+12 |
| 2 |
| 12+32 |
| 10 |
所以,三边之比为
| 2 |
| 10 |
| 2 |
| 5 |
在△ABC中,AC=
| 22+32 |
| 13 |
| 32+82 |
| 73 |
所以,三边之比为
| 13 |
| 73 |
在△HGR中,HG=
| 22+22 |
| 2 |
| 22+62 |
| 10 |
所以,三边之比为2
| 2 |
| 10 |
| 2 |
| 5 |
所以,与△FDE相似的三角形是△HGR.
故答案为:△HGR.
点评:本题考查了相似三角形的判定,勾股定理的应用,根据网格结构,利用勾股定理求出三个三角形的三边的长度,再求出三边的比是解题的关键.

练习册系列答案
相关题目
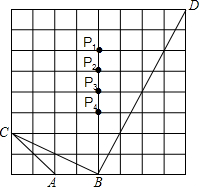 如图,在正方形网格上,若使△ABC∽△PBD,则点P应在( )处.
如图,在正方形网格上,若使△ABC∽△PBD,则点P应在( )处.| A、P1 | B、P2 | C、P3 | D、P4 |
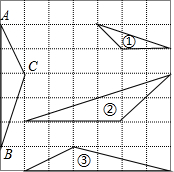 如图,在正方形网格上的三角形①,②,③中,与△ABC相似的三角形有
如图,在正方形网格上的三角形①,②,③中,与△ABC相似的三角形有 如图,在正方形网格上有△ABC和△DEF.
如图,在正方形网格上有△ABC和△DEF. 作图计算题.
作图计算题.