题目内容
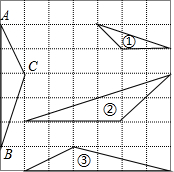 如图,在正方形网格上的三角形①,②,③中,与△ABC相似的三角形有
如图,在正方形网格上的三角形①,②,③中,与△ABC相似的三角形有分析:分别求得各个三角形的边长,从而根据三组对应边的比相等的三个三角形相似来进行判定.
解答:解:△ABC的各边长为:AC=
,BC=
,AB=5
①各边长为:
,2,
②各边长为:2
,4,2
③各边长为:
,
,6
根据如果两个三角形的三组对应边的比相等,那么这两个三角形相似.可得与△ABC相似的三角形有①,②共2个.
| 5 |
| 10 |
①各边长为:
| 2 |
| 10 |
②各边长为:2
| 2 |
| 10 |
③各边长为:
| 5 |
| 17 |
根据如果两个三角形的三组对应边的比相等,那么这两个三角形相似.可得与△ABC相似的三角形有①,②共2个.
点评:此题考查了相似三角形的判定和性质,①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;
②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;
③如果两个三角形的两个对应角相等,那么这两个三角形相似.平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似.
②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;
③如果两个三角形的两个对应角相等,那么这两个三角形相似.平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似.

练习册系列答案
相关题目
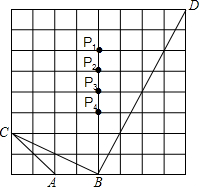 如图,在正方形网格上,若使△ABC∽△PBD,则点P应在( )处.
如图,在正方形网格上,若使△ABC∽△PBD,则点P应在( )处.| A、P1 | B、P2 | C、P3 | D、P4 |
 如图,在正方形网格上有三个三角形,则与△FDE相似的三角形是
如图,在正方形网格上有三个三角形,则与△FDE相似的三角形是 如图,在正方形网格上有△ABC和△DEF.
如图,在正方形网格上有△ABC和△DEF. 作图计算题.
作图计算题.