题目内容
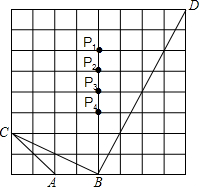如图，在正方形网格上，若使△ABC∽△PBD，则点P应在（ ）处．| A、P1 | B、P2 | C、P3 | D、P4 |
分析：根据相似三角形的判定：三对边分别对应成比例的两个三角形相似来进行判定．
解答：解：若设每个小正方形的边长为1，
则AC：AB：BC=
：1：
，
要使PD：PB：BD=
：1：
，点P只能在P3处，
故选：C．
则AC：AB：BC=
| 2 |
| 5 |
要使PD：PB：BD=
| 2 |
| 5 |
故选：C．
点评：考查相似三角形的判定定理：三边对应成比例的两个三角形相似．
练习册系列答案
相关题目
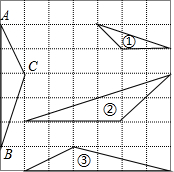如图，在正方形网格上的三角形①，②，③中，与△ABC相似的三角形有
如图，在正方形网格上有三个三角形，则与△FDE相似的三角形是
如图，在正方形网格上有△ABC和△DEF．
作图计算题．