Question

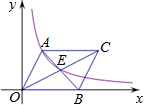
如图为某游乐场电车轨道的一部分ABC的图象，AB为线段，BC为反比例函数y=

k

x

的一部分，已知A（10，1）、B（8，2）、C（2，y_c）．过轨道图象上一点分别作x、y轴垂线才能固定轨道，若垂线段的和（用S表示）取最小值的点称为最佳支撑点．
（1）求直线AB的解析表示式及k值．
（2）求轨道图象最佳支撑点的坐标．

Answer 1

（1）设过A、B的直线为y=kx+b．
将A（10，1）、B（8，2）代入，
得

10k+b=1 8k+b=2

，
解得

k=- 1 2 b=6

，
∴y=-

1

2

x+6；
∵反比例函数y=

k

x

经过点B（8，2），
∴k=8×2=16；

（2）分两种情况：
①设P（x，-

1

2

x+6）是线段AB上任意一点，则8≤x≤10，P到x、y轴距离分别为-

1

2

x+6，x，
∴S=-

1

2

x+6+x=

1

2

x+6，
∵

1

2

＞0，∴S随自变量x的增大而增大，
∴当x=8时，S取最小值，此时S=

1

2

×8+6=10；
②设P（x，

16

x

）是曲线BC上任意一点，则2≤x≤8，P到x、y轴距离分别为

16

x

，x，
∴S=

16

x

+x=（

x

-

4

x

）²+8≥8，
∴当

x

-

4

x

=0，即x=4时，S取最小值，此时S=8．
∵10＞8，
∴最佳支撑点为（4，4）．