题目内容
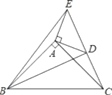
【题目】如图,在Rt△ABC中,∠ACB=90°,CD与CE分别是斜边AB上的高与中线,以下判断中正确的个数有( )
①∠DCB=∠A;②∠DCB=∠ACE;③∠ACD=∠BCE;④∠BCE=∠BEC.
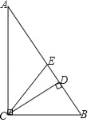
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
根据垂直的定义得到∠CDB=90°,根据余角的性质得到∠DCB=∠A,故①正确;根据直角三角形的性质得到AE=CE=BE,根据等腰三角形的性质得到∠A=∠ACE,于是得到∠DCB=∠ACE,故②正确;同理得到∠ACD=∠BCE,故③正确;由于BC不一定等于BE,于是得到∠BCE不一定等于∠BEC,故④错误.
∵CD⊥AB,
∴∠BDC=90°,
∴∠DCB+B=90°,
∵∠A+∠B=90,
∴∠DCB=∠A,
∴①正确;
∵CE是RtABC斜边AB上的中线,
∴EA=EC=EB,
∴∠ACE=∠A,
∴∠DCB=∠A,
∴∠DCB=∠ACE,
∴②正确;
∵EC=EB,
∴∠B=∠BCE,
∵∠A+∠B=90,∠A+∠ACD=90,
∴∠B= ∠ACD,
∴∠ACD= ∠BCE,
∴③正确;
∵BC与BE不一定相等,
∴∠BCE 与∠BEC 不一定相等,
∴④不正确;
∴正确的个数为3个,
故答案为:C.

练习册系列答案
相关题目