题目内容
先阅读下列解题过程,然后解答问题(1)、(2)、(3).
例:解绝对值方程:|2x|=1.
解:讨论:①当x≥0时,原方程可化为2x=1,它的解是x= .
.
②当x<0时,原方程可化为-2x=1,它的解是x=- .
.
∴原方程的解为x= 和-
和- .
.
问题(1):依例题的解法,方程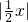 =3的解是______;
=3的解是______;
问题(2):尝试解绝对值方程:2|x-2|=6;
问题(3):在理解绝对值方程解法的基础上,解方程:|x-2|+|x-1|=3.
解:(1)| x|=3,
x|=3,
①当x≥0时,原方程可化为 x=3,它的解是x=6;
x=3,它的解是x=6;
②当x<0时,原方程可化为- x=3,它的解是x=-6;
x=3,它的解是x=-6;
∴原方程的解为x=6和-6,
故答案为:x=6和-6.
(2)2|x-2|=6,
①当x-2≥0时,原方程可化为2(x-2)=6,它的解是x=5;
②当x-2<0时,原方程可化为-2(x-2)=6,它的解是x=-5;
∴原方程的解为x=5和-5.
(3)|x-2|+|x-1|=3,
①当x-2≥0,即x≥2时,原方程可化为x-2+x-1=3,它的解是x=3;
②当x-1≤0,即x≤1时,原方程可化为2-x+1-x=3,它的解是x=0;
③当1<x<2时,原方程可化为2-x+x-1=3,此时方程无解;
∴原方程的解为x=3和0.
分析:(1)分为两种情况:①当x≥0时,②当x<0时,去掉绝对值符号后求出即可.
(2)分为两种情况:①当x-2≥0时,②当x-2<0时,去掉绝对值符号后求出即可.
(3)分为三种情况:①当x-2≥0,即x≥2时,②当x-1≤0,即x≤1时,③当1<x<2时,去掉绝对值符号后求出即可.
点评:本题考查了含绝对值符号的一元一次方程的应用,关键是能去掉绝对值符号,用了分类讨论思想.
 x|=3,
x|=3,①当x≥0时,原方程可化为
 x=3,它的解是x=6;
x=3,它的解是x=6;②当x<0时,原方程可化为-
 x=3,它的解是x=-6;
x=3,它的解是x=-6;∴原方程的解为x=6和-6,
故答案为:x=6和-6.
(2)2|x-2|=6,
①当x-2≥0时,原方程可化为2(x-2)=6,它的解是x=5;
②当x-2<0时,原方程可化为-2(x-2)=6,它的解是x=-5;
∴原方程的解为x=5和-5.
(3)|x-2|+|x-1|=3,
①当x-2≥0,即x≥2时,原方程可化为x-2+x-1=3,它的解是x=3;
②当x-1≤0,即x≤1时,原方程可化为2-x+1-x=3,它的解是x=0;
③当1<x<2时,原方程可化为2-x+x-1=3,此时方程无解;
∴原方程的解为x=3和0.
分析:(1)分为两种情况:①当x≥0时,②当x<0时,去掉绝对值符号后求出即可.
(2)分为两种情况:①当x-2≥0时,②当x-2<0时,去掉绝对值符号后求出即可.
(3)分为三种情况:①当x-2≥0,即x≥2时,②当x-1≤0,即x≤1时,③当1<x<2时,去掉绝对值符号后求出即可.
点评:本题考查了含绝对值符号的一元一次方程的应用,关键是能去掉绝对值符号,用了分类讨论思想.

练习册系列答案
相关题目