题目内容
请先阅读下列解题过程,再解答问题.
已知 x2+x-1=0,求x3+2x2+3的值.
解:x3+2x2+3=x3+x2-x+x2+x+3=x(x2+x-1)+x2+x-1+4=0+0+4=4.
如果1+x+x2+x3=0,求x+x2+x3+x4+x5+x6+x7+x8的值.
已知 x2+x-1=0,求x3+2x2+3的值.
解:x3+2x2+3=x3+x2-x+x2+x+3=x(x2+x-1)+x2+x-1+4=0+0+4=4.
如果1+x+x2+x3=0,求x+x2+x3+x4+x5+x6+x7+x8的值.
分析:所求式子结合后,提取公因式变形,将已知等式代入计算即可求出值.
解答:解:∵1+x+x2+x3=0,
∴原式=(x+x2+x3+x4)+(x5+x6+x7+x8)
=x(1+x+x2+x3)+x5(1+x+x2+x3)
﹦0.
∴原式=(x+x2+x3+x4)+(x5+x6+x7+x8)
=x(1+x+x2+x3)+x5(1+x+x2+x3)
﹦0.
点评:此题考查了因式分解的应用,将所求式子进行适当的变形是解本题的关键.

练习册系列答案
相关题目
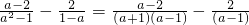 …第一步
…第一步 …第二步
…第二步