��Ŀ����
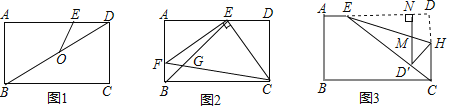
����Ŀ����ͼ���ھ���ABCD�У�AB=3��BC=5��E��AD�ϵ�һ�����㣮
��1����ͼ1������BD��O�ǶԽ���BD���е㣬����OE����OE=DEʱ����AE�ij���
��2����ͼ2������BE��EC������E��EF��EC��AB�ڵ�F������CF����BE���ڵ�G����BEƽ����ABCʱ����BG�ij���
��3����ͼ3������EC����H��CD�ϣ�������ABCD��ֱ��EH�۵����۵����D����EC�ϵĵ�D'��������D����D��N��AD�ڵ�N����EH���ڵ�M����AE=1��
����![]() ��ֵ��
��ֵ��
������BE����D'MH����CBE�Ƿ����ƣ���˵�����ɣ�
���𰸡���1��AE=![]() ����2��BG=
����2��BG=![]() ����3����
����3����![]() �������ƣ����ɼ�����.
�������ƣ����ɼ�����.
��������
��1�������BD���������OD=OB=OA�����жϳ���ODE�ס�ADO�����ɵó����ۣ�
��2�����жϳ���AEF�ա�DCE���������BF=1�����жϳ���CHG�ס�CBF���������BK=GK=![]() ������ù��ɶ������ɵó����ۣ�
������ù��ɶ������ɵó����ۣ�
��3���������EC=5�������D'C=1�����ݹ��ɶ������DH=![]() ��CH=
��CH=![]() �����жϳ���EMN�ס�EHD���ó�
�����жϳ���EMN�ס�EHD���ó�![]() ����ED'M�ס�ECH���ó�
����ED'M�ס�ECH���ó�![]() �������ó�
�������ó�![]() �����ɵó����ۣ�
�����ɵó����ۣ�
�����жϳ���MD'H=��NED'�������жϳ���MD'H=��ECB�����ɵó�![]() �����ɣ�
�����ɣ�
��1����ͼ1������OA��
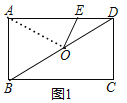
�ھ���ABCD�У�CD=AB=3��AD=BC=5����BAD=90��
��Rt��ABD�У����ݹ��ɶ����ã�BD=![]() ��
��
��O��BD�е㣬
��OD=OB=OA=![]() ��
��
���OAD=��ODA��
��OE=DE��
���EOD=��ODE��
���EOD=��ODE=��OAD��
���ODE�ס�ADO��
��![]() ��
��
��DO2=DEDA��
����AE=x��
��DE=5��x��
����![]() ��2=5��5��x����
��2=5��5��x����
��x=![]() ��
��
����AE=![]() ��
��
��2����ͼ2��
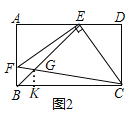
�ھ���ABCD�У�
��BEƽ�֡�ABC��
���ABE=��EBC=45�㣬
��AD��BC��
���AEB=��EBC��
���ABE=��AEB��
��AE=AB=3��
��AE=CD=3��
��EF��EC��
���FEC=90�㣬
���AEF+��CED=90�㣬
�ߡ�A=90�㣬
���AEF+��AFE=90�㣬
���CED=��AFE��
�ߡ�D=��A=90�㣬
���AEF�ա�DCE��
��AF=DE=2��
��BF=AB��AF=1��
����G��GK��BC��K��
���EBC=��BGK=45�㣬
��BK=GK����ABC=��GKC=90�㣬
�ߡ�KCG=��BCF��
���CHG�ס�CBF��
��![]() ��
��
��BK=GK=y��
��CK=5��y��
��y=![]() ��
��
��BK=GK=![]() ��
��
��Rt��GKB��BG=![]() ��
��
��3�����ھ���ABCD�У���D=90�㣬
��AE=1��AD=5��
��DE=4��
��DC=3��
��EC=5��
���۵�֪��ED'=ED=4��D'H=DH����ED'H=��D=90�㣬
��D'C=1��
��D'H=DH=z��
��HC=3��z��
���ݹ��ɶ����ã���3��z��2=1+z2��
��z=![]() ��
��
��DH=![]() ��CH=
��CH=![]() ��
��
��D'N��AD��
���AND'=��D=90�㣬
��D'N��DC��
���EMN�ס�EHD��
��![]() ��
��
��D'N��DC��
���ED'M=��ECH��
�ߡ�MED'=��HEC��
���ED'M�ס�ECH��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
�����ƣ����ɣ����۵�֪����EHD'=��EHD����ED'H=��D=90�㣬
���MD'H+��ED'N=90�㣬
�ߡ�END'=90�㣬
���ED'N+��NED'=90�㣬
���MD'H=��NED'��
��D'N��DC��
���EHD=��D'MH��
���EHD'=��D'MH��
��D'M=D'H��
��AD��BC��
���NED'=��ECB��
���MD'H=��ECB��
��CE=CB=5��
��![]()
���D'MH�ס�CBE��

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ��ij��˾��ƸְԱ�������Լס��ҡ�������������ѡ�˽����˱��Ժ����ԣ�����ɼ����־�Ϊ100�֣�Ȼ���ٰ�����ռ60%������ռ40%�����ѡ�˵��ۺϳɼ�������Ϊ100�֣���
���ǵĸ���ɼ����±���ʾ��
������ | ���Գɼ�/�� | ���Գɼ�/�� |
�� | 90 | 88 |
�� | 84 | 92 |
�� | x | 90 |
�� | 88 | 86 |
��1��ֱ��д����������ѡ�����Գɼ�����λ����
��2���ֵ�֪��ѡ�˱����ۺϳɼ�Ϊ87.6�֣������x��ֵ��
��3���������������ѡ�˵��ۺϳɼ��������ۺϳɼ�����ȷ����Ҫ��Ƹ��ǰ��������ѡ��