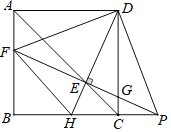
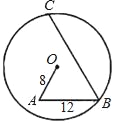
��Ŀ����
����Ŀ������������֮��ľ��������Ӧ������ľ���ֵ,������A��B��ʾ�����ֱ�Ϊa��b,������֮��ľ���ΪAB=![]() ����:��ʾ��1��5������֮��ľ���ɱ�ʾΪ
����:��ʾ��1��5������֮��ľ���ɱ�ʾΪ![]() ����ʾ��-2��3������֮��ľ���ɱ�ʾΪ
����ʾ��-2��3������֮��ľ���ɱ�ʾΪ![]() .
.
��1�������ϱ�ʾ2��7������֮��ľ������� ��,�����ϱ�ʾ3��-6������֮��ľ������� ����
��2�������ϱ�ʾx��-2������M��N֮��ľ������� ��,���![]() ����xΪ�� ����
����x�� ����
��3����ʽ�ӣ�![]() ȡ��Сֵʱ��x��ֵΪ�� ��,��СֵΪ .
ȡ��Сֵʱ��x��ֵΪ�� ��,��СֵΪ .
���������ᣬ����ͼ�Σ�д�����̣�
���𰸡���1����2-7����5����3-��-6������9����2����x+2����-8��4����3��3��6.
��������
��1���ͣ�2����Ҫ�Ǹ�������������֮��ľ���������Ӧ������ľ���ֵ��ֱ���ýϴ������ȥ��С���������м��㣻
��3���������������ľ�����з�����
�⣺��1�������ϱ�ʾ3��8������֮��ľ����ǣ�|2-7|=5��
�����ϱ�ʾ-3��-9������֮��ľ����ǣ�|3-��-6��| =9��
�ʴ�Ϊ��5��9��
��2�������ϱ�ʾx��-2������M��N֮��ľ����ǣ�|x+2|��
���|MN|=6����|x+2|=6��
��x+2=��6��
��ã�x=4��x=-8��
�ʴ�Ϊ��|x+2|��4��-8��
��3��|x+2|+|x-3|+|x-4|�ļ��������ǣ������ϱ�ʾ��x�ĵ㵽��ʾ-2��3��4����
��ľ���֮�ͣ�
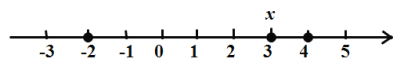
��Ȼֻ�е�x=3ʱ��![]() ȡ����Сֵ��
ȡ����Сֵ��
�൱x=3ʱ��
��СֵΪ��![]() ��
��

����Ŀ��һ�κ���y=mx+n�뷴��������y=![]() ������mn��0��m��n��Ϊ������������ͬһ����ϵ�е�ͼ������ǣ�������
������mn��0��m��n��Ϊ������������ͬһ����ϵ�е�ͼ������ǣ�������
A.  B.
B. 
C. 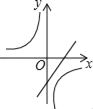 D.
D. 
����Ŀ��Ϊ������Ӧ�����ﴫͳ�Ļ����ĺ��٣�ijѧУ����ȫУ1200��ѧ�����о���ʫ���б�������ڻ֮��ٰ쾭��ʫ�ʴ�����Ϊ�˽Ȿ��ϵ�л�ij���Ч����ѧУ��ί�ڻ����֮���������ȡ����ѧ�����顰һ��ʫ���б������������ݵ��������Ƴɵ�ͳ��ͼ(����)����ͼ��ʾ��

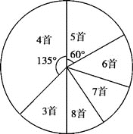
����������һ���£��ٴε����ⲿ��ѧ����һ��ʫ���б������������Ƴ�ͳ�Ʊ���
һ��ʫ���б����� | 3�� | 4�� | 5�� | 6�� | 7�� | 8�� |
�� �� | 10 | 10 | 15 | m | 25 | 20 |
����ݵ������Ϣ
(1)���ε����ȡ�˶�����ѧ����
(2)��ȫ����ͳ��ͼ��������ͳ��ͼ�У���6�ס���Բ�Ľ�Ϊ �ȣ�
(3)������m��ֵΪ ��
(4)����������һ���¸�Уѧ��һ��ʫ���б�6��(��6��)���ϵ�������
����Ŀ��ѧУͨ�������������Ӽס��ҡ������������Ƽ�һ����Ϊ�ؼ��Ƚ��༯�壬�±�����������������ʿ����÷ֱ���
�������ʿ����÷ֱ�����λ���֣�
�༶ | ��Ϊ�淶 | ѧϰ�ɼ� | У�˶��� | ������ | �Ͷ����� |
�װ� | 10 | 10 | 6 | 10 | 7 |
�Ұ� | 10 | 8 | 8 | 9 | 8 |
���� | 9 | 10 | 9 | 6 | 9 |
����ͳ�Ʊ��е���Ϣ�ش��������⣺
��1�����㲹ȫ����ɼ������������е����ݣ�
�༶ | ƽ���� | ���� | ��λ�� |
�װ� | 8.6 | 10 | �� |
�Ұ� | 8.6 | �� | 8 |
���� | �� | 9 | 9 |
��2�������ϱ��е����ݣ����Ƽ��ĸ���Ϊ�ؼ��Ƚ��༯�壿��˵�����ɡ�
��3�����ѧУ����Ϊ�淶��ѧϰ�ɼ���У�˶��ᡢ�������Ͷ�����������ɼ�����3��2��1��1��3�ı�ȷ���༶���ۺϳɼ���ѧ����������ʦ��������ۺϳɼ���������һ��������������ͳ��ͼ���뽫���ͳ��ͼ������������������ɼ���Ӧ�Ƽ��ĸ���Ϊ�ؼ��Ƚ��༯�壿Ϊʲô��