题目内容
【题目】在Rt△ABC中,∠ACB=90°,AC=BC,D为边AB中点,点E、F分别在射线CA、BC上,且AE=CF,连结EF.
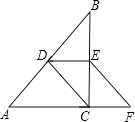
猜想:如图①,当点E、F分别在边CA和BC上时,线段DE与DF的大小关系为________.
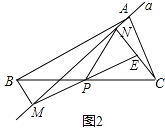
探究:如图②,当点E、F分别在边CA、BC的延长线上时,判断线段DE与DF的大小关系,并加以证明.
应用:如图②,若DE=4,利用探究得到的结论,求△DEF的面积.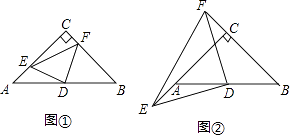
【答案】猜想:DE=DF.
如图1,连结CD,
∵∠ACB=90°,AC=BC,
∴∠CAD=45°,
∵D为边AB的中点,
∴CD=AD,∠BCD= ![]() ∠ACB=45°,
∠ACB=45°,
∴∠EAD=∠FCD,
在△AED和△CFD中
∴△ADE≌△CFD(SAS),
∴DE=DF,
故答案为:DE=DF;
探究:DE=DF,证明如下:
如图2,连接CD,
∵∠ACB=90°,AC=BC,
∴∠CAD=45°,
∵D为AB中点,
∴AD=CD,∠BCD= ![]() ∠ACB=45°,
∠ACB=45°,
∵∠CAD+∠EAD=∠BCD+∠FCD=180°,
∴∠EAD=∠FCD=135°,
在△ADE和△CDF中
∴△ADE≌△CDF(SAS),
∴DE=DF;
应用:
∵△ADE≌△CDF,
∴∠ADE=∠CDF,
∵∠ADC=90°,
∴∠EDF=90°,
∵DE=DF=4,
∴S△DEF= ![]() DE2=
DE2= ![]() ×42=8.
×42=8.
【解析】猜想:连接CD,可证明△ADE≌△CFD,可得出结论;探究:连接CD,同(1)可证明△ADE≌△CFD,可证得DE=DF;应用:由△ADE≌△CFD可证得∠EDF=90°,容易求得△DEF的面积.
【考点精析】本题主要考查了全等三角形的性质的相关知识点,需要掌握全等三角形的对应边相等; 全等三角形的对应角相等才能正确解答此题.

练习册系列答案
相关题目