[题目]如图.在平面直角坐标系中.点A在函数y=﹣ 的图象上.点B在函数y= 的图象上.点C在x轴上．若四边形OABC为平行四边形.则△OBC的面积为．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在平面直角坐标系中，点A在函数y=﹣ （x＜0）的图象上，点B在函数y= （x＞0）的图象上，点C在x轴上．若四边形OABC为平行四边形，则△OBC的面积为．

【答案】3
【解析】解：过A作AE⊥x轴于点E，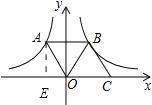

设A（a，b），B（x，b），
∵点A在反比例函数y=﹣ 上，点B在反比例函数y= 上，
∴ab=﹣2，xb=4，
∴x=﹣2a，
∴AB=|﹣2a﹣a|=3a，
∵四边形OABC是平行四边形，
∴CO=AB=3a，
∴四边形OABC的面积是：COBE=6ab=6，
△OBC的面积为=3，
所以答案是：3．
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识，掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分．

练习册系列答案

(1)求出营销员的个人月收入y(元)与该营销员每月的销售量x(万件)(x≥0)之间的函数关系式；

(2)已知该公司营销员李平5月份的销售量为1.2万件，求李平5月份的收入．

【题目】如图，在四边形ABCD中，BC＞BA，AD=CD，BD平分∠ABC，

求证：∠A+∠C=180°．

【题目】如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O，与BC相交于点N，连接BM、DN．

（1）求证：四边形BMDN是菱形；
（2）若AB=4，AD=8，求菱形BMDN的面积和对角线MN的长．

【题目】如图甲，四边形OABC的边OA、OC分别在x轴、y轴的正半轴上，顶点在B点的抛物线交x轴于点A、D，交y轴于点E，连接AB、AE、BE．已知tan∠CBE= ，A（3，0），D（﹣1，0），E（0，3）．

（1）求抛物线的解析式及顶点B的坐标；
（2）求证：CB是△ABE外接圆的切线；
（3）试探究坐标轴上是否存在一点P，使以D、E、P为顶点的三角形与△ABE相似，若存在，直接写出点P的坐标；若不存在，请说明理由；
（4）设△AOE沿x轴正方向平移t个单位长度（0＜t≤3）时，△AOE与△ABE重叠部分的面积为s，求s与t之间的函数关系式，并指出t的取值范围．

【题目】如图，为了测量某交通路口设立的路况显示牌的立杆AB的高度，在D处用高1.2m的测角仪CD，测得最高点A的仰角为32°，已知观测点D到立杆AB的距离DB为3.8m，求立杆AB的高度．（结果精确到0.1m）
【参考数据：sin32°=0.53，cos32°=0.85，tan32°=0.62】

【题目】在Rt△ABC中，∠ACB=90°，AC=BC，D为边AB中点，点E、F分别在射线CA、BC上，且AE=CF，连结EF．
猜想：如图①，当点E、F分别在边CA和BC上时，线段DE与DF的大小关系为________．
探究：如图②，当点E、F分别在边CA、BC的延长线上时，判断线段DE与DF的大小关系，并加以证明．
应用：如图②，若DE=4，利用探究得到的结论，求△DEF的面积．

【题目】已知D、E分别为△ABC中AB、BC上的动点，直线DE与直线AC相交于F，∠ADE的平分线与∠B的平分线相交于P，∠ACB的平分线与∠F的平分线相交于Q．

（1）如图1，当F在AC的延长线上时，求∠P与∠Q之间的数量关系；

（2）如图2，当F在AC的反向延长线上时，求∠P与∠Q之间的数量关系（用等式表示）．

【题目】如图，∠AOB＝45，∠AOB内有一定点P，且OP＝10．在OA上有一动点Q，OB上有一动点R．若ΔPQR周长最小，则最小周长是（）

A. 10 B. C. 20 D.

试题分类