题目内容
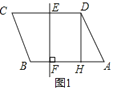
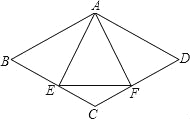
【题目】.如图 1,B、D 分别是 x 轴和 y 轴的正半轴上的点,AD∥x 轴,AB∥y 轴(AD>AB),点 P 从 C 点出发,以 3cm/s 的速度沿 CDAB 匀速运动,运动到 B 点时终止;点 Q 从 B 点出发,以 2cm/s 的速度,沿 BCD 匀速运动,运动到 D 点时终止.P、Q 两点同时出发, 设运动的时间为 t(s),△PCQ 的面积为 S(cm2),S 与 t 之间的函数关系由图 2 中的曲线段 OE,线段 EF、FG 表示.
(1)求 AD 点的坐标;
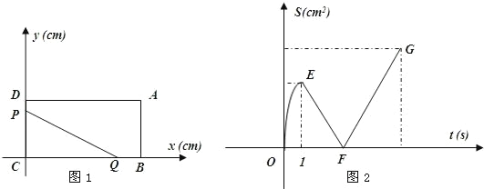
(2)求图2中线段FG的函数关系式;
(3)是否存在这样的时间 t,使得△PCQ 为等腰三角形?若存在,直接写出 t 的值;若不存在, 请说明理由.
【答案】(1) D(0,3), A(6,3);(2) ![]() ;(3)
;(3)![]() ,
,![]() ,
,![]()
【解析】
(1)由图象可知CD=3×1=3,设AD=BC=a,根据点Q到达点C时,点P到达点A,列出方程即可求出a.
(2)当点Q在CD上,点P在AB上时,对应的函数图象是线段FG,由此即可解决问题.
(3)分三种情形讨论:①Q在BC上,P在CD上时,列出方程即可;
②Q在BC上,P在AD上时,由CP=CQ得6﹣2t![]() ,整理得5t2+6t﹣18=0解方程即可;
,整理得5t2+6t﹣18=0解方程即可;
由PQ=CQ得![]() 6﹣2t,整理得7t2﹣22t+18=0,△<0,无解.当PC=PQ得6﹣2t=2(3t﹣3),解得t
6﹣2t,整理得7t2﹣22t+18=0,△<0,无解.当PC=PQ得6﹣2t=2(3t﹣3),解得t![]() ;
;
③Q在CD上,P在AB上时,由CP=PQ列出方程即可.
(1)设AD=BC=a,由图象可知CD=AB=3,点Q到达点C时,点P到达点A,否则P、Q继续运动时,S与t的函数图象不是直线,∴![]() ,∴a=6,∴点A坐标(6,3),点D坐标(0,3).
,∴a=6,∴点A坐标(6,3),点D坐标(0,3).
(2)当点Q在CD上,点P在AB上时,对应的函数图象是线段FG,∴S![]() CQ6=3CQ=3(2t﹣6)=6t﹣18.
CQ6=3CQ=3(2t﹣6)=6t﹣18.
(3)分三种情况讨论:
①Q在BC上,P在CD上时,由CP=CQ得6﹣2t=3t,解得:t![]() (不合题意舍弃,
(不合题意舍弃,![]() 1);
1);
②Q在BC上,P在AD上时,由CP=CQ得:6﹣2t![]() ,整理得5t2+6t﹣18=0,t
,整理得5t2+6t﹣18=0,t![]() 或
或![]() (舍弃).
(舍弃).
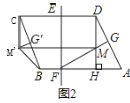
由PQ=CQ,如图1.
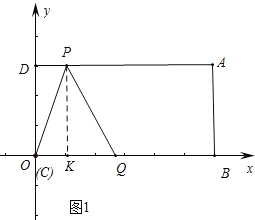
作PK⊥OB于K,则DP=OK=3t﹣3,KQ=6﹣2t﹣(3t﹣3)=9﹣5t,∴PQ![]() ,∴
,∴![]() 6﹣2t,整理得7t2﹣22t+18=0,△<0,无解.
6﹣2t,整理得7t2﹣22t+18=0,△<0,无解.
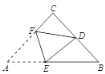
当PC=PQ.如图2.
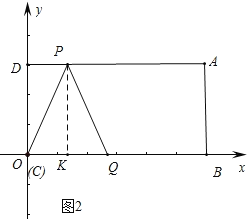
作PK⊥OB于K,则OK=KQ=DP,∴OQ=2DP,∴6﹣2t=2(3t﹣3),解得t![]() ;
;
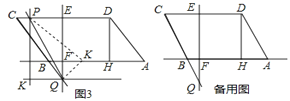
③Q在CD上,P在AB上时,由CP=PQ,如图3.
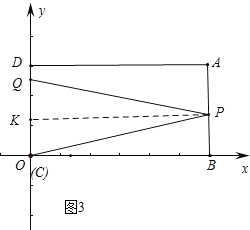
作PK⊥OD于K,则KQ=OK=PB,∴2PB=OQ,∴2(12﹣3t)=2t﹣6,解得:t![]() .
.
综上所述t![]() s或
s或![]() s或
s或![]() s时,△PCQ为等腰三角形.
s时,△PCQ为等腰三角形.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案