题目内容
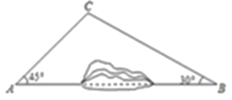
【题目】为加快城乡对接,建设美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山.汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=100千米,∠A=45°,∠B=30°.
(1)开通隧道前,汽车从A地到B地要走多少千米?
(2)开通隧道后,汽车从A地到B地可以少走多少千米?(结果保留根号)
【答案】(1) ![]() 千米;(2)
千米;(2)![]() 千米.
千米.
【解析】
![]() 过点C作AB的垂线CD,垂足为D,在直角
过点C作AB的垂线CD,垂足为D,在直角![]() 中,解直角三角形求出CD,进而解答即可;
中,解直角三角形求出CD,进而解答即可;
![]() 在直角
在直角![]() 中,解直角三角形求出BD,再求出AD,进而求出答案.
中,解直角三角形求出BD,再求出AD,进而求出答案.
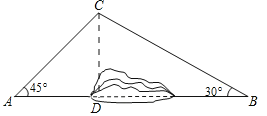
解:(1)过点C作AB的垂线CD,垂足为D,
![]() ,
,![]() ,
,![]() 千米,
千米,![]() (千米),
(千米),![]() 千(米),
千(米),![]() 千米,
千米,
答:开通隧道前,汽车从A地到B地要走![]() 千米;
千米;
(2)![]() ,
,![]() (千米),
(千米),![]() (千米),
(千米),![]() (千米),
(千米),![]() ,
,![]() (千米),
(千米),![]() 千米,
千米,
答:开通隧道后,汽车从A地到B地可以少走![]() 千米.
千米.

练习册系列答案
相关题目