题目内容
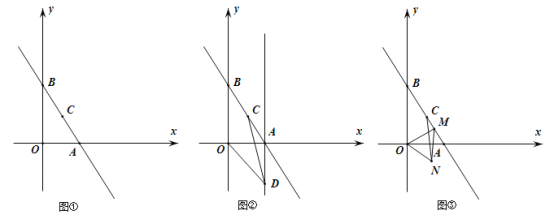
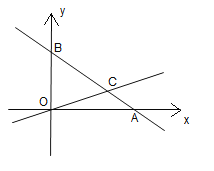
【题目】如图,在平面直角坐标系中,过点![]() 的直线
的直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)分别求出直线![]() 、直线
、直线![]() 的表达式;
的表达式;
(2)在直线![]() 上是否存在一点P,使得
上是否存在一点P,使得![]() ?若存在,求出此时点
?若存在,求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)直线OC表达式: ![]() ;直线AB表达式:
;直线AB表达式: ![]() ;(2)P的坐标(3,2)或(﹣3,6)
;(2)P的坐标(3,2)或(﹣3,6)
【解析】
(1)利用待定系数法求出各表达式即可.
(2)先根据题目的条件解出S△OCP,再设出P点横坐标代入求出,再将横坐标代入AB表达式即可.
(1)设直线OC的表达式为:y=kx,
将![]() 代入得:
代入得:![]() ,解得
,解得![]() ,
,
∴直线OC的表达式为: ![]() .
.
∵AB过点(0,4),设直线AB的表达式为:y=kx+4,
将![]() 代入得:
代入得:![]() ,解得
,解得![]() ,
,
∴直线AB的表达式为: ![]() .
.
(2) 存在, P的坐标为(3,2)或(﹣3,6),理由如下:
![]() ,
,
设P点横坐标Px,则![]() ,
,
解得Px=±3,
将x=3代入![]() ,解得y=2,
,解得y=2,
将x=﹣3代入![]() ,解得y=6,
,解得y=6,
∴P的坐标为(3,2)或(﹣3,6).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目