Question

【题目】在平面直角坐标系中，直线分别与轴、轴交于两点，点为线段的中点．

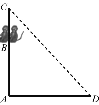
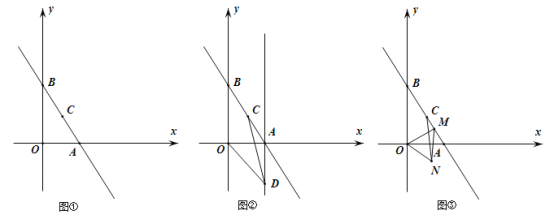
（1）如图①，点的坐标为（ ， ），点的坐标为（ ， ）， ；

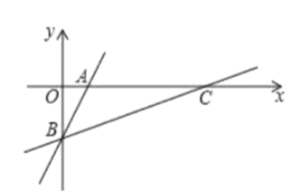
（2）如图②，若点是经过点，且与轴平行的直线上的一个动点，求的最小值；

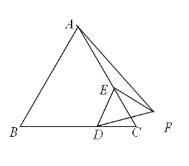
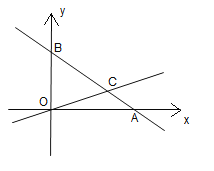
（3）如图③，点是线段上一动点，以为边在的下方作等边，连接，求的最小值．

Answer 1

【答案】(1)0,3;,0;60;(2)最小值为:3;(3)最小值为:2

【解析】

(1)分别令x=0,y=0代入求解即可得出A、B的值,再利用正切求出角度即可．

(2)作点O关于直线AD的对称点E,连接CE交直线AD于D’,此时OD+CD的值最小,分别求出C点和E点的坐标,利用勾股定理求出CE即可．

(3)以OA为边长向下作等边△AOD,可以确定N的运动方向在ON上,再作C点关于ON的点E,连接OE则ON+CN的最小值就是OE．

(1)令x=0,代入,解得y=3,则B(0,3),

令y=0,代入,解得x=,则A(,0),

,则∠OAB=60°．

故答案为: 0,3;,0;60．

(2)作点O关于直线AD的对称点E,连接CE交直线AD于D’,此时OD+CD的值最小．

∵C是AB的中点,

∴C()即C(),

∵OA=,

∴OE=2,

CE=．

(3)由(1)可知∠OAC=60°,以OA为边长向下作等边△OAD,连接OC,则△AOC也为等边三角形,作C点关于DA直线的对称点E,由于DA恰好是∠CAE的角平分线,故E正好落在x轴上．则OE就为ON+CN的最小值．

根据角平分线的性质,可得AE=AC,

由等边△AOC可得AC=AO=,

∴ON+CN的最小值:OE=2．