题目内容
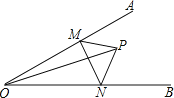
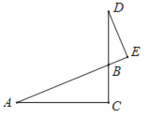
【题目】如图,∠ACB=90°,AC=CD,过点D作AB的垂线交AB的延长线于点E.若AB=2DE,则∠BAC的度数为________.
【答案】22.5°
【解析】
连接AD,延长AC、DE交于M,求出∠CAB=∠CDM,根据全等三角形的判定得出△ACB≌△DCM,求出AB=DM,求出AD=AM,根据等腰三角形的性质得出即可.
解: 连接AD,延长AC、DE交于M,

∵∠ACB=90°,AC=CD,
∴∠DAC=∠ADC=45°,
∵∠ACB=90°,DE⊥AB,
∴∠DEB=90°=∠ACB=∠DCM,
∵∠ABC=∠DBE,
∴由三角形内角和定理得:∠CAB=∠CDM,
在△ACB和△DCM中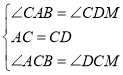
∴△ACB≌△DCM(ASA),
∴AB=DM,
∵AB=2DE,
∴DM=2DE,
∴DE=EM,
∵DE⊥AB,
∴AD=AM,
∴∠BAC=∠DAE=![]() ∠DAC=
∠DAC=![]() ×45°=22.5°,
×45°=22.5°,
故答案为:22.5°

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目