题目内容
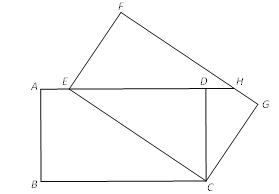
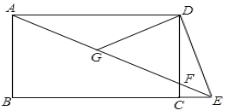
【题目】如图,点E是矩形ABCD的边BC延长线上一点,连接AE,交CD于点F,G是AF的中点,再连接DG、DE,且DE=DG.
(1)求证:∠DEA=2∠AEB;
(2)若BC=2AB,求∠AED的度数。
【答案】(1)证明见解析(2)45°
【解析】
(1)根据直角三角形斜边中线的性质可求出AG=DG,所以∠DAG=∠ADG,再利用矩形的性质和三角形的外角和定理即可证明:∠DEA=2∠AEB;
(2)过点作GH⊥DC于H,则∠DCE=∠GFH=3∠AEB=3∠DAE,所以∠DAE+∠GFH=90°,所以4∠DAE=90°,∠DAE=22.5°,进而得到∠DEA=2∠DAE=45°.
(1)∵四边形ABCD是矩形,
∴∠ADF=90,AD∥BC,
∵Rt△ADF中,G是AF中点,
∴GA=GD=GF,
∴∠DGF=2∠DAE,
∵AD∥BE,
∴∠AEB=∠DAE,
∵DG=DE,
∴∠DEA=∠DGF,
∴∠DEA=2∠AEB;
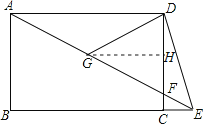
(2) 过点作GH⊥DC于H,
∵AD∥GH,G是AF中点,
则GH=![]() AD=AB=DC,
AD=AB=DC,
又∵DE=DG=GF,
∴Rt△GHF≌Rt△DCE(HL),
∵∠DEA=2∠AEB,
∴∠DCE=∠GFH=3∠AEB=3∠DAE,
∵∠DAE+∠GFH=90°,
∴4∠DAE=90°,
∠DAE=22.5°,
∴∠DEA=2∠DAE=45°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目