题目内容
【题目】阅读理解:

(1)已知x3+27有一个因式x+3,用待定系数法分解:x3+27.
(2)观察上述因式分解,直接写出答案:因式分解:a3+b3=_______;a3-b3=________.
【答案】(1)x+27=(x+3)(x-3x+9);(2)(a+b)(a-ba+ b);(a-b)(a+ba+ b)
【解析】
(1)根据x3 +27=(x+3)(x2+ax+b),得出有关a,b的方程组求出即可;
(2)根据a3+b3=(a+b)(a+ma+n),得出有关m,n的方程组求出即可;
根据a3-b3=(a-b)(a+ma+n),得出有关m,n的方程组求出即可.
解:(1)∵(x+3)(x+ax+b)=x+(a+3)x+(b+3a)x+3b
∴ a+3=0
b+3a=0 即a=-3,b=9
3b=27
因此x+27=(x+3)(x-3x+9)
(2)∵(a+b)(a+ma+n)=a+(m+b)a+(n+bm)a+bn
∴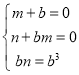
解得:![]()
因此a3+b3=(a+b)(a-ba+ b)
∵(a-b)(a+ma+n)=a+(m-b)a+(n-bm)a-bn
∴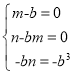
解得:![]()
因此a3-b3=(a-b)(a+ba+ b)
故答案为:(a+b)(a-ba+ b);(a-b)(a+ba+ b)

练习册系列答案
相关题目