题目内容
【题目】如图,在三角形ABC中,CE⊥AB于E,DF⊥AB于F,AC∥ED,CE是∠ACB的平分线,试比较∠EDF与∠BDF的大小,并说明理由.
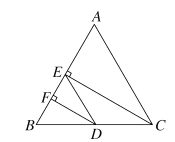
【答案】∠EDF=∠BDF
【解析】试题分析:先根据平行线的性质得出∠ACE=∠DEC,再运用垂直于同一条直线的两直线平行得出DF∥CE,进而利用平行线的性质得出∠BDF=∠BCE,∠FDE=∠DEC,然后利用角平分线等量代换即可得出两角的关系.
试题解析:
解:∠EDF=∠BDF.
理由如下:∵AC∥ED,∴∠ACE=∠DEC.
∵CE⊥AB,DF⊥AB,∴∠AEC=∠AFD=90°,
∴DF∥CE,∴∠BDF=∠BCE,∠FDE=∠DEC,
∴∠FDE=∠ACE.
∵CE平分∠ACB,∴∠ECB=∠ACE.
∴∠EDF=∠BDF.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目