题目内容
【题目】如图,P1是一块半径为1的半圆形纸板,在P1的左下端剪去一个半径为 ![]() 的半圆后得到图形P2 , 然后依次剪去一个更小的半圆(其直径为前一个被剪掉半圆的半径)得图形P3 , P4 , …,Pn , …,记纸板Pn的面积为Sn , 试通过计算S1 , S2 , 猜想得到Sn﹣1﹣Sn=(n≥2).
的半圆后得到图形P2 , 然后依次剪去一个更小的半圆(其直径为前一个被剪掉半圆的半径)得图形P3 , P4 , …,Pn , …,记纸板Pn的面积为Sn , 试通过计算S1 , S2 , 猜想得到Sn﹣1﹣Sn=(n≥2). 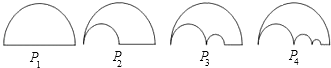
【答案】( ![]() )2n﹣1π
)2n﹣1π
【解析】解:根据题意得,n≥2.S1= ![]() π×12=
π×12= ![]() π,
π,
S2= ![]() π﹣
π﹣ ![]() π×(
π×( ![]() )2 ,
)2 ,
…
Sn﹣1= ![]() π﹣
π﹣ ![]() π×(
π×( ![]() )2﹣
)2﹣ ![]() π×[(
π×[( ![]() )2]2﹣…﹣
)2]2﹣…﹣ ![]() π×[(
π×[( ![]() )n﹣2]2 ,
)n﹣2]2 ,
Sn= ![]() π﹣
π﹣ ![]() π×(
π×( ![]() )2﹣
)2﹣ ![]() π×[(
π×[( ![]() )2]2﹣…﹣
)2]2﹣…﹣ ![]() π×[(
π×[( ![]() )n﹣2]2﹣
)n﹣2]2﹣ ![]() π×[(
π×[( ![]() )n﹣1]2 ,
)n﹣1]2 ,
∴Sn﹣1﹣Sn= ![]() π×(
π×( ![]() )2n﹣2=(
)2n﹣2=( ![]() )2n﹣1π.
)2n﹣1π.
故答案为( ![]() )2n﹣1π.
)2n﹣1π.
由P1是一块半径为1的半圆形纸板,在P1的左下端剪去一个半径为 ![]() 的半圆后得到图形P2 , 得到S1=
的半圆后得到图形P2 , 得到S1= ![]() π×12=
π×12= ![]() π,S2=
π,S2= ![]() π﹣
π﹣ ![]() π×(
π×( ![]() )2 . 同理可得Sn﹣1=
)2 . 同理可得Sn﹣1= ![]() π﹣
π﹣ ![]() π×(
π×( ![]() )2﹣
)2﹣ ![]() π×[(
π×[( ![]() )2]2﹣…﹣
)2]2﹣…﹣ ![]() π×[(
π×[( ![]() )n﹣2]2 , Sn=
)n﹣2]2 , Sn= ![]() π﹣
π﹣ ![]() π×(
π×( ![]() )2﹣
)2﹣ ![]() π×[(
π×[( ![]() )2]2﹣…﹣
)2]2﹣…﹣ ![]() π×[(
π×[( ![]() )n﹣2]2﹣
)n﹣2]2﹣ ![]() π×[(
π×[( ![]() )n﹣1]2 , 它们的差即可得到.
)n﹣1]2 , 它们的差即可得到.

练习册系列答案
相关题目