题目内容
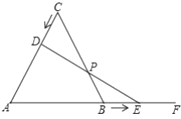
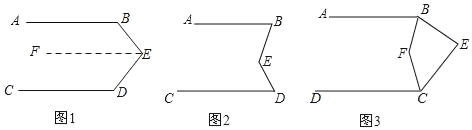
【题目】(1)如图①,在等边△ABC中,点M是BC边上的任意一点(不含端点B,C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ACN=∠ABC.
【类比探究】
(2)如图②,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ACN=∠ABC还成立吗?请说明理由.
【拓展延伸】
(3)如图③,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.

【答案】(1)答案见解析;(2)∠ACN=∠ABC还成立;(3)∠ABC=∠ACN.
【解析】试题分析:(1)利用SAS可证明△BAM≌△CAN,继而得出结论;
(2)也可以通过证明△BAM≌△CAN,得出结论,和(1)的思路完全一样.
(3)首先得出∠BAC=∠MAN,从而判定△ABC∽△AMN,得到![]() ,根据∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,得到∠BAM=∠CAN,从而判定△BAM∽△CAN,即可得出结论.
,根据∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,得到∠BAM=∠CAN,从而判定△BAM∽△CAN,即可得出结论.
试题解析:解:(1)∵△ABC、△AMN是等边三角形,∴AB=AC,AM=AN,∠BAC=∠MAN=60°,∴∠BAM=∠CAN,在△BAM和△CAN中,∵AB=AC,∠BAM=∠CAN,AM=AN,∴△BAM≌△CAN(SAS),∴∠ABC=∠ACN.
(2)结论∠ABC=∠ACN仍成立;
理由如下:∵△ABC、△AMN是等边三角形,∴AB=AC,AM=AN,∠BAC=∠MAN=60°,∴∠BAM=∠CAN,在△BAM和△CAN中,∵AB=AC,∠BAM=∠CAN,AM=AN,∴△BAM≌△CAN(SAS),∴∠ABC=∠ACN.
(3)∠ABC=∠ACN;
理由如下:∵BA=BC,MA=MN,顶角∠ABC=∠AMN,∴底角∠BAC=∠MAN,∴△ABC∽△AMN,∴ ![]() ,又∵∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,∴∠BAM=∠CAN,∴△BAM∽△CAN,∴∠ABC=∠ACN.
,又∵∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,∴∠BAM=∠CAN,∴△BAM∽△CAN,∴∠ABC=∠ACN.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:

(说明:成绩80分及以上为优秀,![]() 分为良好,
分为良好,![]() 分为合格,60分以下为不合格)
分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:70707071727373737475767778
这一组的是:70707071727373737475767778
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分(单位:分) | 中位数(单位:分) | 众数(单位:分) |
甲 | 74.2 |
| 85 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)上表中n的值为_____.
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是___校的学生(填“甲”或“乙”),请说明理由.
【题目】为改善生态环境,防止水土流失,某村计划在江汉堤坡种植白杨树,现甲、乙两家林场有相同的白杨树苗可供选择,其具体销售方案如下:
甲林场 | 乙林场 | ||
购树苗数量 | 销售单价 | 购树苗数量 | 销售单价 |
不超过1000棵时 | 4元/棵 | 不超过2000棵时 | 4元/棵 |
超过1000棵的部分 | 3.8元/棵 | 超过2000棵的部分 | 3.6元/棵 |
设购买白杨树苗x棵,到两家林场购买所需费用分别为y甲(元)、y乙(元).
(1)该村需要购买1500棵白杨树苗,若都在甲林场购买所需费用为 元,若都在乙林场购买所需费用为 元;
(2)分别求出y甲、y乙与x之间的函数关系式;
(3)如果你是该村的负责人,应该选择到哪家林场购买树苗合算,为什么?