��Ŀ����
����Ŀ����1�����ں�������д�ʵ������ݣ��������Ľ����̣�
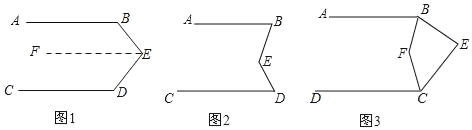
��ͼ���������ABE+��BED+��CDE��360�㣬��˵��AB��CD��
���ɣ�����E��EF��AB
���ԡ�ABE+��BEF���� ���㣨�� ����
������ABE+��BED+��CDE��360��
���ԡ�FED+��CDE���� ����
����EF���� ��.
����ΪEF��AB,
����AB��CD.
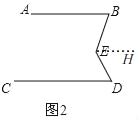
��2����ͼ�������AB��CD����˵����BED����B+��D��
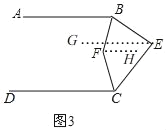
��3����ͼ�������AB��CD����BEC������BFƽ�֡�ABE��CFƽ�֡�DCE�����BFC�Ķ������� �����ú����Ĵ���ʽ��ʾ����
���𰸡���1��180����ֱ��ƽ�У�ͬ���ڽǻ�����180��CD����2������������3��180�㩁![]() ����
����
��������
��1�����жϳ���FED+��CDE=180���ó�EF��CD�����ɵó����ۣ�
��2�����жϳ���BEH=��B�����жϳ�EH��CD���ó���DEH=��D�����ɵĵó����ۣ�
��3�����жϳ���ABE+��DCE=360��-���������жϳ���ABF+��DCF=180��-![]() ����������2���Ľ��ۼ��ɵó����ۣ�
����������2���Ľ��ۼ��ɵó����ۣ�
��:��1������E��EF��AB
���ABE+��BEF��180���� ��ֱ��ƽ�У�ͬ���ڽǻ�����
�ߡ�ABE+��BED+��CDE��360��
���FED+��CDE��180��
��EF��CD
��EF��AB
��AB��CD��
�ʴ�Ϊ��180����ֱ��ƽ�У�ͬ���ڽǻ�����180��CD��
��2����ͼ2��
����E��EH��AB��
���BEH����B��
��EH��AB��AB��CD��
��EH��CD��
���DEH����D��
���BED����BEH+��DEH����B+��D��
��3����ͼ3��
����E��EG��AB��
���ABE+��BEG��180����
��EG��AB��CD��AB��
��EG��CD��
���DCE+��CEG��180��
���ABE+��BEG+��CEG+��DCE��360����
���ABE+��BEC+��DCE��360����
���ABE+��DCE��360������BEC��
�ߡ�BEC������
���ABE+��CCE��360��������
��BF��CF�ֱ�ƽ�֡�ABE����DCE��
���ABE��2��ABF����DCF��2��ECF��
���ABF+��DCF��180����![]() ����
����
����F����FH��AB��
ͬ��2���ķ����ã���BFC����ABF+��DCF��180����![]() ����
����
�ʴ�Ϊ��180����![]() ����
����