ЬтФПФкШн
ЁОЬтФПЁПЮЊНЈЩшУРРіМвдАЃЌФГЩчЧјНЋЯНЧјФкЕФ-ПщУцЛ§ЮЊ1000m2ЕФПеЕиНјааТЬЛЏЃЌ-ВПЗжжжВнЃЌЪЃгрВПЗжддЛЈЃЌЩшжжВнВПЗжЕФУцЛ§ЮЊx(m2)ЃЌжжВнЫљашЗбгУyl(дЊ)гыx(m2)ЕФКЏЪ§ЙиЯЕЭМЯѓШчЭМЫљЪОЃЌддЛЈЫљашЗбгУy2(дЊ)гыx(m2)ЕФКЏЪ§ЙиЯЕЪНЮЊy2=-0.Olx2-20x+30000(0ЁмxЁм1000)ЃЎ
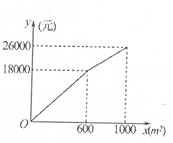
(1)Чѓyl(дЊ)гыx(m2)ЕФКЏЪ§ЙиЯЕЪНЃЛ
(2)ЩшетПщ1000m2ПеЕиЕФТЬЛЏзмЗбгУЮЊW(дЊ)ЃЌЧыРћгУWгыxЕФКЏЪ§ЙиЯЕЪНЃЌЧѓТЬЛЏзмЗбгУWЕФзюДѓжЕЃЎ
ЁОД№АИЁП(1)МћНтЮіЃЛ(2)W=0.01x2+36000ЃЌWШЁзюДѓжЕЮЊ32500дЊ.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнКЏЪ§ЭМЯѓРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓЕУy1ЃЈдЊЃЉгыxЃЈm2ЃЉЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉзмЗбгУЮЊW=y1+y2ЃЌСаГіКЏЪ§ЙиЯЕЪНМДПЩЧѓНт.
ЃЈ1ЃЉЕБ0x<600ЪБЃЌЩшКЏЪ§НтЮіЪНЮЊy1=k1xЃЌ
НЋx=600ЁЂy=18000ЕУЃК600k1=18000ЃЌ
НтжЎЃКk1=30ЃЌ
Ёрy1=30xЃЌ
ЕБ600x1000ЪБЃЌЩшy1=k2x+bЃЌ
НЋx=600ЁЂy=18000КЭx=1000ЁЂy=26000ДњШыЗжБ№ДњШыЕУЃК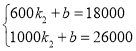 ЃЌ
ЃЌ
НтжЎЃК![]() ЃЌ
ЃЌ
Ёрy1=20x+6000ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ0x<600ЪБЃЌ
W=30x+(0.01x220x+30000)=0.01x2+10x+30000ЃЌ
Ёп0.01<0ЃЌ
W=0.01(x500)2+32500ЃЌ
ЁрЕБx=500ЪБЃЌWШЁЕУзюДѓжЕЮЊ32500дЊЃЛ
ЕБ600x1000ЪБЃЌ
W=20x+6000+(0.01x220x+30000)=0.01x2+36000ЃЌ
Ёп0.01<0ЃЌ
ЁрЕБ600x1000ЪБЃЌWЫцxЕФдіДѓЖјМѕаЁЃЌ
ЁрЕБx=600ЪБЃЌWШЁзюДѓжЕЮЊ32400ЃЌ
Ёп32400<32500ЃЌ
ЁрWШЁзюДѓжЕЮЊ32500дЊ,,

 ЪжРЪжШЋгХСЗПМОэЯЕСаД№АИ
ЪжРЪжШЋгХСЗПМОэЯЕСаД№АИ